Skip over navigation
Some points never touch, other points touch only once, other points touch twice.
Contact
Age 14 to 16
Challenge Level 
|
When the disc is in the corner there is one quarter of the
circumference (that is a length $2\pi/4 = \pi/2$) which does not
come in contact with the edge of the tray. As the disc rolls round
one circuit:
an arc of length $2$ units comes into contact,
then an arc of length $\pi/2$ gets missed,
then an arc of length $1$ unit comes into contact,
then an arc of length $\pi/2$ gets missed,
then an arc of length $2$ units comes into contact,
then an arc of length $\pi/2$ gets missed,
then an arc of length $1$ unit comes into contact.
|
 |
Some points never touch, other points touch only once, other points touch twice.
As an extension to this problem, can you now work out how much of the circumference of the disc never touches the edge of the tray?
The article 'A Rolling Disc' discusses variations of this problem.
You may also like
Just Rolling Round
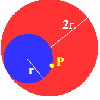
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
Coke Machine
The coke machine in college takes 50 pence pieces. It also takes a certain foreign coin of traditional design...
Just Opposite
A and C are the opposite vertices of a square ABCD, and have coordinates (a,b) and (c,d), respectively. What are the coordinates of the vertices B and D? What is the area of the square?