Skip over navigation

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Platonic Planet
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This problem gives learners the opportunity to use their
visualisation skills to investigate different paths over the
surface of a solid. Tackling the challenge of finding the shortest
path offers a chance to practise trigonometry, as well as
encouraging justification that there is no better path than the one
they find.
Possible approach
Start with a cube and investigate nets and paths.
How about an octahedron?
Next, ask everyone to imagine they were standing on the
surface of a dodecahedron. Ask what they can see if they are
standing on a face, on an edge, or on a vertex.
One way of introducing the idea of paths on the surface of the
dodecahedron is to have a model of a dodecahedron which can be
drawn on and then unfolded into its net. Alternatively, the path
could be drawn on a net and learners will need to imagine how the
parts of the path will meet up when the net is folded up, to make
sure it really is a closed path.
The pictures of nets shown in the problem are not necessarily
the easiest nets to use to draw the path, so it is worth drawing
out discussion of what would be a good net to use in order to aid
visualisation.
Once everyone is happy with the idea of closed paths on the
surface of the dodecahedron, learners can start to create their own
paths and calculate the lengths. At each stage, they should be
challenging themselves to see whether there is any way they can
make the path shorter while still being able to see every part of
the planet's surface.
In order to compare answers within the classroom, it is
important for the class to decide how long one side of the planet
will be. This could be a good opportunity to discuss the idea of
working things out in terms of a unit length.
Key questions
How much of the planet's surface can I see if I stand at a
face, an edge, a vertex?
Is it easier to investigate this problem using some nets
rather than others?
Possible extension
The Dodecahedron provides an opportunity for further exploration of paths on the surface.Possible support
Use accurate scale drawing to calculate path lengths rather than trigonometry.You may also like
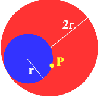
Just Rolling Round
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
Coke Machine
The coke machine in college takes 50 pence pieces. It also takes a certain foreign coin of traditional design...
Just Opposite
A and C are the opposite vertices of a square ABCD, and have coordinates (a,b) and (c,d), respectively. What are the coordinates of the vertices B and D? What is the area of the square?

