Skip over navigation
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Golden Triangle
Age 16 to 18
Challenge Level 





- Problem
- Student Solutions
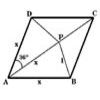
| The three triangles are all isoceles so $ \angle BDC = \angle ACB = \angle ABC. $ |
 |
$ \angle BDC = \angle BAC + \angle DBA = 2 \angle BAC. $
$ \angle BCD + \angle ABC + \angle BAC = \angle BDC + \angle
BDC + \angle BAC = 180^o. $
$ 2 \angle BAC + 2 \angle BAC + \angle BAC = 180^o $
$ 5 \angle BAC = 180^o $,
$ \angle BAC = \angle DBA = 36^o$,
$\angle BDA = 108^o $ ,
$ \angle ABC = \angle ACB = \angle BDC = 72^o $
and $ \angle CBD = 36^o. $
The triangles $ ABC $ and $ BDC $ have lengths $ AB = AC = p $
and $ BC = BD = DA = q $ and the angles are $ 36^o , 72^o $ and $
72^o $ so they are similar triangles. Taking the ratio of
corresponding sides $ AC/BC = BC/DC $ : $$\frac{p}{q} =
\frac{q}{p-q}$$ So $ p^2 -pq-q^2 = 0 $ and dividing by $ q^2 $
gives the quadratic equation $$(p/q)^2 -(p/q)-1=0 $$ which has the
solutions $(1 \pm \sqrt 5) /2$. We don't want the negative root for
such a ratio as it would make no sense. Hence $ p/q = (\sqrt{5} +
1)/2 $. Similarly $ q/p = (\sqrt 5 - 1)/2 $.
Triangles $ ABC $ and $ BDC $ are similar and the ratio of
areas is the square of the ratio of corresponding sides. So area
of
$ BDC : ABC $ $ = [(\sqrt 5 - 1)^2/2 ] : 1 $
$ = (6 -2\sqrt 5 )/4 : 1 $
$ = (3 - \sqrt 5 ) : 2 $
So if the area of triangle $ ABC $ is $2$ the area of triangle
$ BDC $ is $3-\sqrt 5$ and the area of triangle $ ABD $ is $ 2 - (3
- \sqrt 5) = \sqrt 5 -1 $.
You may also like
Gold Again
Without using a calculator, computer or tables find the exact values of cos36cos72 and also cos36 - cos72.
Pythagorean Golden Means
Show that the arithmetic mean, geometric mean and harmonic mean of a and b can be the lengths of the sides of a right-angles triangle if and only if a = bx^3, where x is the Golden Ratio.

