Skip over navigation
Richard sent us his work on this problem.
Strange Rectangle
Age 16 to 18
Challenge Level 
Richard sent us his work on this problem.
- We can say that $A P S$ and $B Q P$ are similar triangles
(ratio of sides same), so in terms of angles:
$\angle A P S =\angle B Q P$
$ = 180^{\circ} - 90^{\circ} - \angle B P Q$ (angles in triangle add to $180^{\circ}$)
$=90^{\circ} - \angle B P Q$
$\angle S P Q + \angle A P S + \angle B P Q = 180^{\circ}$ (angles from a point on a straight line add to $180^{\circ}$)
$\Rightarrow \angle S P Q + (90^{\circ} - \angle B P Q) + \angle B P Q = 180^{\circ}$
$\Rightarrow \angle S P Q + 90^{\circ} = 180^{\circ}$
$\Rightarrow \angle S P Q = 90^{\circ}$. - Same applies again here, triangle $Q C R$ is similar to $R D
S$, and so in terms of angles:
$\angle C R Q = \angle D S R$
$ = 90^{\circ} - \angle S R D$
$\angle S R Q + \angle C R Q + \angle S R D = 180^{\circ}$
$\angle S R Q + (90^{\circ} - \angle S R D) + \angle S R D = 180^{\circ}$
$\angle S R Q = 90^{\circ}$. - As two opposite angles add up to $180^{\circ}$, the other two must as well (angles in quadrilateral add up to $360^{\circ}$). Two pairs of opposite angles each adding to $180^{\circ}$ implies a cyclic quadrilateral (one of the Circle Theorems).
-
Firstly, as $\angle S P Q$ and $\angle S R Q$ are both $90^{\circ}$, line $S Q$ must be the diameter of the circle with midpoint being centre of circle, $M$.
As $A P R D$ is a rectangle, $\angle A P R$ and $\angle D R P$ are both right angles. Also lines $P M = R M$, as $P$ and $R$ are on the circle.
Midpoint $M$ is also the centre of the rectangle. Let $V$ be the length of the perpendicular from $M$ to side $A B$, and let $U$ be the length from the foot of this perpendicular to $P$, as shown in the diagram.
$U = [y(x-y) + x(x+y)]/2 - A P$
$ = [x y - y^2 + x^2 + x y]/2 - y(x-y)$
$= [x^2 + y^2]/2$
$V = [y(x+y) + x(x-y)]/2$
$ = [x y + y^2 + x^2 -x y]/2$
$ = [x^2 + y^2]/2$
As $U = V$, $\angle B P M = 45^{\circ}$
$\Rightarrow \angle R P M = 45^{\circ}$
$\Rightarrow \angle P R M = 45^{\circ}$ (isosceles triangle)
$\Rightarrow \angle P M R = 180^{\circ} - 45^{\circ} - 45^{\circ}= 90^{\circ}$
$\Rightarrow \angle P Q R = 45^{\circ}$ (angle at centre is double that at edge - Circle Theorem) - As $\angle P Q R = 45^{\circ}$
$\Rightarrow \angle P S R = 180^{\circ} - 45^{\circ}$ (Cyclic Quadrilateral)
$ = 135^{\circ}$.
You may also like
Set Square
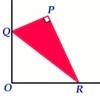
A triangle PQR, right angled at P, slides on a horizontal floor with Q and R in contact with perpendicular walls. What is the locus of P?
Biggest Bendy
Four rods are hinged at their ends to form a quadrilateral. How can you maximise its area?
Strange Rectangle 2
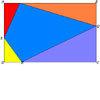
Find the exact values of some trig. ratios from this rectangle in which a cyclic quadrilateral cuts off four right angled triangles.