Skip over navigation
This solution is from Yatir Halevi.
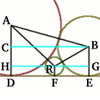
Let $a$, $b$ and $c$ be the radii the circles centered at $A$, $B$ and $C$ respectively.
Angle $BOC = 90^\circ$ since, $OB$ is tangent to the circle centered at $C$ and hence it is perpendicular to the radius. That also means that the radius of the the circle centered at $O$ is $2c$.
As $BC$ connects $B$ and $C$ it is equal to $b+c$.
By Pythagoras theorem: $(2c-b)^2 + c^2 = (b+c)^2$. Hence $4c^2=6bc$ and $c$ can't be equal to $0$ so $2c=3b$.
We could extend the lines $AC$ and $BO$, to create a mirror image, where we have two circles centered at $A'$ and $B'$ with radii $a'$ and $b'$ respectively, and due to symmetry issues, $a'=a$ and $b'=b$. We will also connect $O$ with $A'$ and $O$ with $A$.
Now $OA=OA'= 2c-a$ and $AC = A'C = c+a$ and so the line $OC$ cuts $A'A$ in half, and because the sides of the triangle $A'OA$ are equal, $OC$ is also perpendicular to $A'A$, hence $\angle OCA = 90$.
As triangle $ACO$ is a right-angled triangle, using Pythagoras' Theorem: $AC^2+OC^2=AO^2$ and so $$(a+c)^2 + c^2 =(2c-a)^2$$ which simplifies to $6ac=2c^2$ and $c$ can't be equal to $0$ so $c=3a$. Combining this with $2c=3b$ we get: $3b=6a$ that is $b=2a$ and so $a=b/2=c/3$, that is they are in the ratio $1:2:3$ as required.
If we mirror the image in the line $BO$ thus creating a new circle below the one centered at $B$, centered at $A''$ it has the same radius as $A$ by symmetry. By the the same line of thought that we used before, we reach the conclusion that $\angle ABO=90$. What we get is that $CABO$ has 3 right angles, meaning that the fourth is also a right angle and that it is a rectangle and that triangle $ABC$ is also right angled.
Let's look at triangle $OBC$ in which $OB = 2c-b = 6a - 2a = 4a$, $OC = c = 3a$ and $BC = b + c = 2a+3a = 5a.$ So the ratio between the sides are $3:4:5$, like we wanted to prove.
Let's look at triangle $ABC$ in which $AB = a + b = a + 2a = 3a$, $AC = a + c = a + 3a = 4a$ and $CB = b + c = 2a + 3a = 5a$. So the ratio between the sides are $3:4:5$, like we wanted to prove.
Arun Iyer proved this result by applying Descartes Circle Theorem.
Retracircles
Age 16 to 18
Challenge Level 
This solution is from Yatir Halevi.
Let $a$, $b$ and $c$ be the radii the circles centered at $A$, $B$ and $C$ respectively.
Angle $BOC = 90^\circ$ since, $OB$ is tangent to the circle centered at $C$ and hence it is perpendicular to the radius. That also means that the radius of the the circle centered at $O$ is $2c$.
As $BC$ connects $B$ and $C$ it is equal to $b+c$.
By Pythagoras theorem: $(2c-b)^2 + c^2 = (b+c)^2$. Hence $4c^2=6bc$ and $c$ can't be equal to $0$ so $2c=3b$.
We could extend the lines $AC$ and $BO$, to create a mirror image, where we have two circles centered at $A'$ and $B'$ with radii $a'$ and $b'$ respectively, and due to symmetry issues, $a'=a$ and $b'=b$. We will also connect $O$ with $A'$ and $O$ with $A$.
Now $OA=OA'= 2c-a$ and $AC = A'C = c+a$ and so the line $OC$ cuts $A'A$ in half, and because the sides of the triangle $A'OA$ are equal, $OC$ is also perpendicular to $A'A$, hence $\angle OCA = 90$.
As triangle $ACO$ is a right-angled triangle, using Pythagoras' Theorem: $AC^2+OC^2=AO^2$ and so $$(a+c)^2 + c^2 =(2c-a)^2$$ which simplifies to $6ac=2c^2$ and $c$ can't be equal to $0$ so $c=3a$. Combining this with $2c=3b$ we get: $3b=6a$ that is $b=2a$ and so $a=b/2=c/3$, that is they are in the ratio $1:2:3$ as required.
If we mirror the image in the line $BO$ thus creating a new circle below the one centered at $B$, centered at $A''$ it has the same radius as $A$ by symmetry. By the the same line of thought that we used before, we reach the conclusion that $\angle ABO=90$. What we get is that $CABO$ has 3 right angles, meaning that the fourth is also a right angle and that it is a rectangle and that triangle $ABC$ is also right angled.
Let's look at triangle $OBC$ in which $OB = 2c-b = 6a - 2a = 4a$, $OC = c = 3a$ and $BC = b + c = 2a+3a = 5a.$ So the ratio between the sides are $3:4:5$, like we wanted to prove.
Let's look at triangle $ABC$ in which $AB = a + b = a + 2a = 3a$, $AC = a + c = a + 3a = 4a$ and $CB = b + c = 2a + 3a = 5a$. So the ratio between the sides are $3:4:5$, like we wanted to prove.
Arun Iyer proved this result by applying Descartes Circle Theorem.
You may also like
Baby Circle
A small circle fits between two touching circles so that all three circles touch each other and have a common tangent? What is the exact radius of the smallest circle?
Kissing
Two perpendicular lines are tangential to two identical circles that touch. What is the largest circle that can be placed in between the two lines and the two circles and how would you construct it?
Logosquares
Ten squares form regular rings either with adjacent or opposite vertices touching. Calculate the inner and outer radii of the rings that surround the squares.