Skip over navigation
Nice construction work from Ashley at Downham Market High School.
First we need the area of the whole circle using the formula $\pi r^2$ to produce $300 \; \text{cm}^2$
Then if $\pi r^2$ is $300$, $r^2$ is $95.49296586$
So $r$ is the square root of $95.49296586$ and has to be $9.8 \;\text{cm}$ to the nearest $\text{mm}$
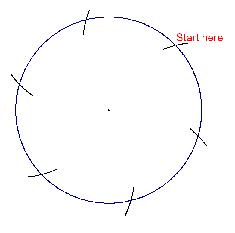
Next join three of the marks to the centre to make thirds
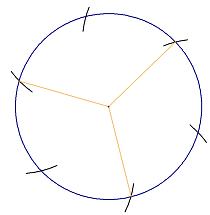
Measure half way along these lines to get the centre for the semi-circles that make the tear shapes.
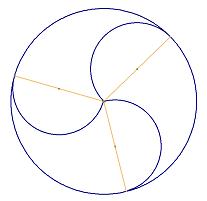
Finally rub out the working and add some colour.
Well done Ashley. Maybe someone can see how to find those mid-points by construction rather than measuring.
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Three Tears
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Nice construction work from Ashley at Downham Market High School.
First we need the area of the whole circle using the formula $\pi r^2$ to produce $300 \; \text{cm}^2$
Then if $\pi r^2$ is $300$, $r^2$ is $95.49296586$
So $r$ is the square root of $95.49296586$ and has to be $9.8 \;\text{cm}$ to the nearest $\text{mm}$
Now draw the circle.
Keeping the radius fixed, move the point of the compasses to the circumference and mark off one radius length around the circumference.
Move the point of the compasses on to that mark and repeat until you have six marks equally spaced around the circle.
Next join three of the marks to the centre to make thirds
Measure half way along these lines to get the centre for the semi-circles that make the tear shapes.
Finally rub out the working and add some colour.
Well done Ashley. Maybe someone can see how to find those mid-points by construction rather than measuring.
You may also like
Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?
Pareq Exists
Prove that, given any three parallel lines, an equilateral triangle always exists with one vertex on each of the three lines.
The Medieval Octagon
Medieval stonemasons used a method to construct octagons using ruler and compasses... Is the octagon regular? Proof please.

