Skip over navigation
This is a game for two players. You need one set of ten Cuisenaire rods between you, like this:
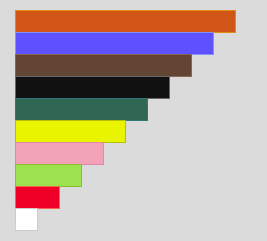
Alternatively, you could use the interactivity below.
This game is called Trains. A train is made by putting rods end to end.
The aim of the game is to be the person who places the last rod to complete a train of a particular length.
Try playing the game lots of times.
Do you think it is better to go first or second? Why?
Tell us about any useful strategies (ways of playing or ways of winning) that you have developed.
If you have another adult in your classroom, you could explain to the class that the two of you are going to play a game, without talking, and that you'd like everyone to watch. Say to learners that, as they watch, you'd like them to think about what they notice and whether they have any questions. (If you don't have an adult, you could brief one of the children beforehand so they know how to play.) Begin to play the game, perhaps so that you both have a couple of moves each and then invite the class to talk to a partner. As a whole group, share comments and queries, so that the rules of the game are established. (You may like to play a few more moves in silence to help clarify anything that has come up initially.)
Set children off in pairs, or threes/fours so that one pair plays against another, either using real Cuisenaire rods or using the interactivity on a tablet or computer. Give them chance to play several times so that they begin to get a 'feel' for the game, then specifically say that you would like them to consider good ways of winning the game as they continue to play. It might be appropriate for you to suggest that everyone has the same length final train to start with to enable initial comparisons to be made more easily. Subsequently, children could move on to wider exploration that might include different length trains.
In the plenary, you could hear about some strategies that different groups have developed, and perhaps try them out using the interactivity. Do they get a sense of whether it is better to go first or second? What evidence do they have to support their view?
Can you win this move? How do you know?
What do you think your opponent will do next if you place that rod?
Train Tactics
Age 7 to 11
Challenge Level 
Train Tactics
This is a game for two players. You need one set of ten Cuisenaire rods between you, like this:
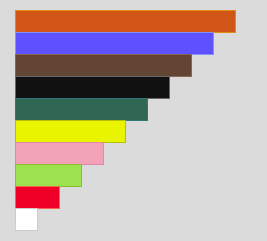
Alternatively, you could use the interactivity below.
This game is called Trains. A train is made by putting rods end to end.
The aim of the game is to be the person who places the last rod to complete a train of a particular length.
- One player decides on the length of the final 'train'. (We suggest this is longer than an orange rod but less than the length of five yellow rods.)
- The other player goes first and chooses a rod.
- The second player then chooses another rod and places it end to end with the first rod so there is a single train.
- Players take it in turns in this way, each placing a new rod on the end of the train to make it longer and longer.
- The player who puts down the last rod to make the chosen length wins.
Try playing the game lots of times.
Do you think it is better to go first or second? Why?
Tell us about any useful strategies (ways of playing or ways of winning) that you have developed.
Why play this game?
This game is an accessible context in which learners can practise addition and subtraction, but crucially it encourages strategic thinking too.Possible approach
If your children are not already familiar with Cuisenaire rods, it is essential to give them time to 'play' with the rods before having a go at this activity.If you have another adult in your classroom, you could explain to the class that the two of you are going to play a game, without talking, and that you'd like everyone to watch. Say to learners that, as they watch, you'd like them to think about what they notice and whether they have any questions. (If you don't have an adult, you could brief one of the children beforehand so they know how to play.) Begin to play the game, perhaps so that you both have a couple of moves each and then invite the class to talk to a partner. As a whole group, share comments and queries, so that the rules of the game are established. (You may like to play a few more moves in silence to help clarify anything that has come up initially.)
Set children off in pairs, or threes/fours so that one pair plays against another, either using real Cuisenaire rods or using the interactivity on a tablet or computer. Give them chance to play several times so that they begin to get a 'feel' for the game, then specifically say that you would like them to consider good ways of winning the game as they continue to play. It might be appropriate for you to suggest that everyone has the same length final train to start with to enable initial comparisons to be made more easily. Subsequently, children could move on to wider exploration that might include different length trains.
In the plenary, you could hear about some strategies that different groups have developed, and perhaps try them out using the interactivity. Do they get a sense of whether it is better to go first or second? What evidence do they have to support their view?
Key questions
Which rod will you place now? Why?Can you win this move? How do you know?
What do you think your opponent will do next if you place that rod?
Possible support
Playing with a partner against another person, or another pair, provides a great opportunity for children to discuss their next move and offers support to build mathematical confidence and problem-solving skills.Possible extension
You could ask learners to begin to generalise the game. How does the length of the final train make a difference to the strategy?You may also like
Cuisenaire Squares
These squares have been made from Cuisenaire rods. Can you describe the pattern? What would the next square look like?
Rod Fractions
Pick two rods of different colours. Given an unlimited supply of rods of each of the two colours, how can we work out what fraction the shorter rod is of the longer one?
