Skip over navigation
The idea for this problem was suggested by Geoff Faux. See also the NRICH Problem 'Polycircles' .
Escriptions
Age 16 to 18
Challenge Level 
The idea for this problem was suggested by Geoff Faux. See also the NRICH Problem 'Polycircles' .
|
Try to visualise necklaces of touching circles centred at the
vertices of a right-angled triangle, first where the circles touch
on the sides of the triangle and then where points of contact lie
on the sides produced. Now try to visualise where these circles
meet the inscribed and escribed circles of the triangle.
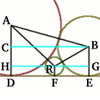
Given any right-angled triangle $ABC$ with sides $a, b$ and
$c$, find the radii of the three circles with centres at $A, B$ and
$C$ such that each circle touches the other two and two of the
circles touch on $AB$ between $A$ and $B$, two circles touch on
$CA$ produced and two circles touch on $CB$ produced.
Now for any right-angled triangle $ABC$ find the radii of the
three escribed circles as shown in the diagram.
|
 |
You may also like
Baby Circle
A small circle fits between two touching circles so that all three circles touch each other and have a common tangent? What is the exact radius of the smallest circle?
Kissing
Two perpendicular lines are tangential to two identical circles that touch. What is the largest circle that can be placed in between the two lines and the two circles and how would you construct it?
Logosquares
Ten squares form regular rings either with adjacent or opposite vertices touching. Calculate the inner and outer radii of the rings that surround the squares.