Skip over navigation
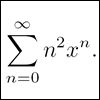

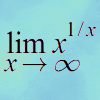
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Quick Route
Age 16 to 18
Challenge Level 





You want to get across a square ploughed field from one corner to the opposite corner as quickly as possible. There is a path along one edge of the field but the rest of the field is ploughed right up to the other three edges. On the ploughed land you can walk at 6 km per hour. From where you are standing you can walk on the path along one edge of the field at 10 km per hour, but there are
no paths along the other edges of the field. What is the best route to take?
Suppose the edge of the field is one kilometre in length. What is the shortest time in which you can cross the field to the opposite corner?
You may also like
Generally Geometric
Generalise the sum of a GP by using derivatives to make the coefficients into powers of the natural numbers.
Bend
What is the longest stick that can be carried horizontally along a narrow corridor and around a right-angled bend?
Exponential Trend
Find all the turning points of y=x^{1/x} for x>0 and decide whether each is a maximum or minimum. Give a sketch of the graph.

