Skip over navigation
Cereal Mix
Age 11 to 14
Challenge Level 
Why do this problem:
A simple problem to get students starting to think about ratio.Possible approach :
Ask students to suggest possible combinations and their suggestions could be written up for everyone in the group to see.Key questions :
-
Do all these combinations cost $ £5$ per kg? How do you find out?
-
Do any of these combinations give identical mixes? How do you find out?
-
Are there any relationships between the quantities of the different ingredients?
Possible extension :
Students can be pressed to explore and articulate more
explicitly the degree of freedom possible within the constraint
that the final mix should cost $ £5$ per kg.
Ask students to include a visualisation of why that result
(ratio relationship for Apricots, Nuts & Seeds) might be
expected.
Possible support :
For students who need more support than the text of the
problem.
Ask each student to generate a result price for a ratio mix of
their own choice.
List these mix costs, with the Apricot / Nut / Seed ratio that
produced them as reference for the next task.
Ask students to find ratios of ingredients that will put a
mixture cost per kg in between each value listed.
You may also like
Rule of Three
If it takes four men one day to build a wall, how long does it take 60,000 men to build a similar wall?
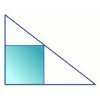
How Big?
If the sides of the triangle in the diagram are 3, 4 and 5, what is the area of the shaded square?