Up and Across
Take a look at the interactivities below which show regular polygons "rolling" along the horizontal surface, leaving a trace of the path of the dot.
In the first interactivity, the graph records the horizontal distance travelled by the dot.
In the second interactivity, the graph records the height of the dot over time.
Experiment by positioning the dot at the centre of the polygons, at one of the vertices or at the centre of one of the sides of the polygons and explore how this affects the two graphs.
Challenge:
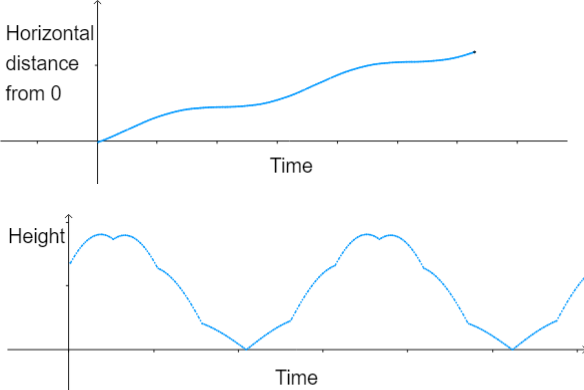
Can you now work out what produced the following two graphs?
Can you work out how many sides the polygon had and where the dot was placed?
Try to explain how you worked it out.
Related Collections
You may also like
Walk and Ride
How far have these students walked by the time the teacher's car reaches them after their bus broke down?
Rolling Around
A circle rolls around the outside edge of a square so that its circumference always touches the edge of the square. Can you describe the locus of the centre of the circle?
N Is a Number
N people visit their friends staying N kilometres along the coast. Some walk along the cliff path at N km an hour, the rest go by car. How long is the road?