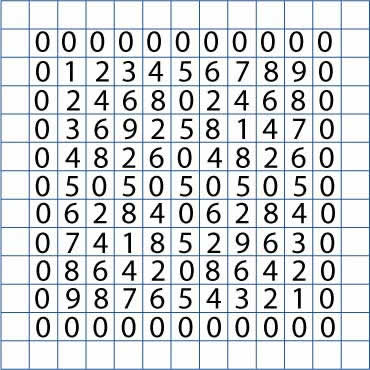
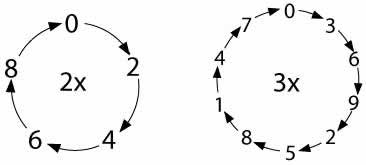
Tables Without Tens

Age 7 to 11

Challenge Level Yellow star

You will need a piece of squared paper for this activity. If you don't have any, you can get a sheet here.

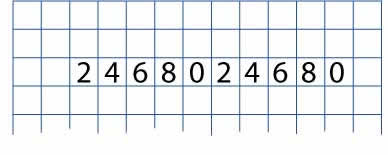
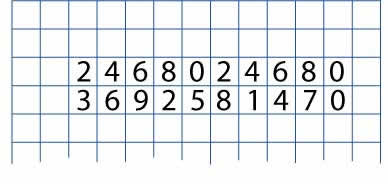
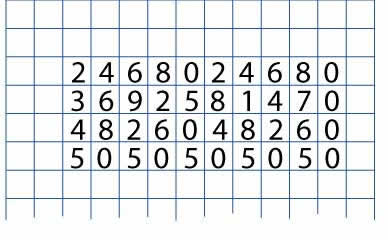
Write the ones digits of the numbers in the two times table from $1 \times 2$ up to $10 \times 2$ in a line. Leave some room at the top of the paper, and some space to the left and right, a bit like this:

You might be able to see some patterns in these numbers.

Now, do the same thing with the multiples of three. Remember, just write the ones digits, this time directly underneath the line of the two times table, like this:

Continue by writing in the four and five times tables in the same way. Again, just using the ones digits.

units digits of two, three, four and five times tables

Now look at the whole array of numbers you have created.

What patterns can you find?

Try to explain why the patterns occur.

What do you notice about these four sets of numbers?

Can you predict what would happen next if we wrote in the next times table?

***************

Well, why not add in the tables of sixes, sevens, eights, nines and finally tens?

After that, for the sake of completeness, we could put in the table of ones and zeros.

Do you have a grid that looks like this?

units digits of all tables from zero to ten

What patterns are there here?

What about repeats?

Can you predict what you will find?

How might you record the repeats that you find?

Each line could be written like this:

units digits of twos and threes in a circular rotation

But you will probably find some other ways which are just as good.

You could try writing all the tables like that.

Are some tables the same or similar to others?

Does it matter which way the arrows go?

What can you discover about the pattern of repeats?

Can you predict what you will find out about 'pairs' of tables?

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Tables Without Tens

You may also like

Exploring Wild & Wonderful Number Patterns

Magazines

Pebbles