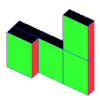
Cuboid-in-a-box

You might want to make a box of the right size first and use some cubes to try out your ideas.

Imagine you put cubes all along the base of the box and they were joined together to make a cuboid. How high would you need to make this cuboid so that you couldn't get another one the same size inside the box?

Instead of imagining putting cubes to fill the base, how about putting cubes up against a different face of the box? How far would you need to extend this cuboid so that you couldn't get another one in the same size?

But does the cuboid need to be touching all of one face?

In fact, does the cuboid need to be put in the box so that it is parallel to the edges?