Domino Sorting

Domino Sorting

Domino Sorting printable sheet

ere are some dominoes taken out of the full set:

 

Sort them into two groups - one group with an odd number of spots and one group with an even number of spots.

Do you have any dominoes left over? Why or why not?

 

Now put the dominoes into pairs. The number of spots on each pair of dominoes must make a total of $5$.

How many pairs can you make?

Which dominoes are left over?

 

Can you pair them up in any different ways so that each pair adds to $5$?

Which dominoes are left over now?

 

Are there any dominoes which are always left over?

Can you explain why?

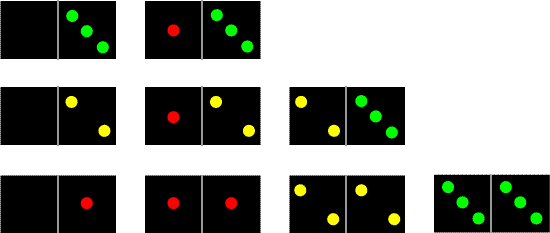
Why do this problem?

This problem will help learners to become more familiar with odd and even numbers, and number bonds to five. It will also challenge them to justify findings.

Possible approach

If you have an interactive whiteboard, you may find our Dominoes Environment useful for this problem.

• How can you sort them?
• Can you make a pattern?
• Can you make a snake?
• What did you notice?

Key questions

Possible extension

You might want some children to find all the different ways of making pairs that add to $5$. This could be by picking two and then replacing them, or by finding all the different combinations which could be made at the same time (the problem as written focuses on the latter). Whichever way, part of their task should be to convince you that they have not missed any pairs out.
Domino Join Up is a similar problem which gives practice in number bonds to six, and could be used as an extension to this problem.

Possible support

Children would really benefit from having sets of dominoes to manipulate as this allows them to change their mind easily, so giving them more confidence to begin the task, and also prevents them from using any domino twice.