Skip over navigation
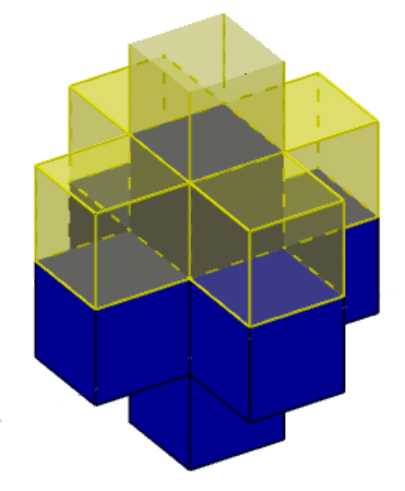
We now glue the yellow faces to the up and bottom faces of the blue cross. We require 5 yellow cubes for wrapping each of the two blue cubes. (We used transparent yellow cubes)
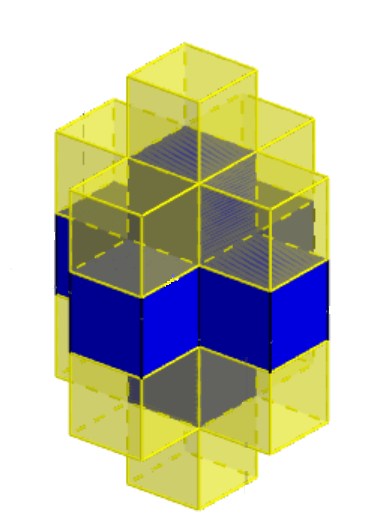
Now we need one yellow cube for each of the four corners:


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Cubic Covering
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
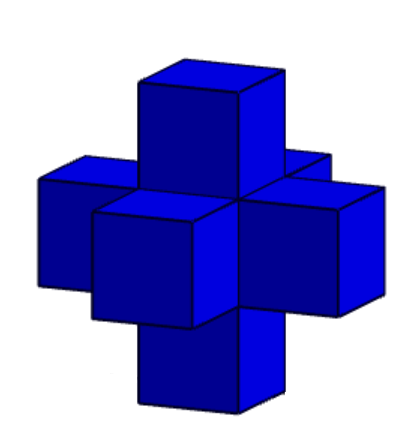
We first imagine the cross with the blue cubes only:

We now glue the yellow faces to the up and bottom faces of the blue cross. We require 5 yellow cubes for wrapping each of the two blue cubes. (We used transparent yellow cubes)


Now we need one yellow cube for each of the four corners:

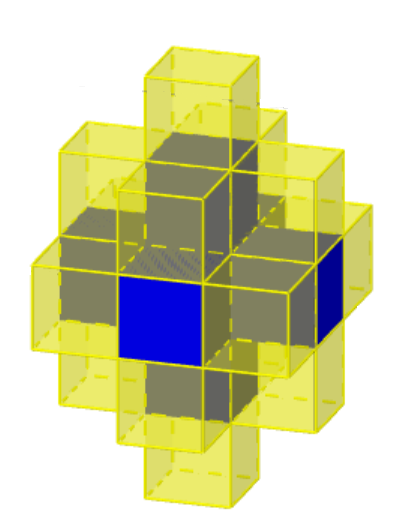
Finally, we have 4 faces to cover, so we need 4 more squares.
Therefore, we used $5+5+4+4 = 18$ yellow cubes.
Therefore, we used $5+5+4+4 = 18$ yellow cubes.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Nine Colours
Can you use small coloured cubes to make a 3 by 3 by 3 cube so that each face of the bigger cube contains one of each colour?
Marbles in a Box
How many winning lines can you make in a three-dimensional version of noughts and crosses?

