Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
The Rescaled Map



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We aim to scale the countries on the map below to represent population size.
We use the hint given and let the ocean keep its original proportion of the map, which is $\frac{39}{64}\times 100=61$ of the map.
| Country | Area (million square kilometres) | Proportion of total land area | Population (millions) | Proportion of total population |
| A | 8 | 0.32 | 40 | 0.4 |
| B | 5 | 0.2 | 36 | 0.36 |
| C | 12 | 0.48 | 24 | 0.24 |
We then find out the factors by which the country sizes need to change:
A needs to cover $\frac{0.4}{0.32}=1.25$ times more area on the map
B needs to cover $\frac{0.36}{0.2}=1.8$ times more area on the map
C needs to cover $\frac{0.24}{0.48}=0.5$ times less area on the map
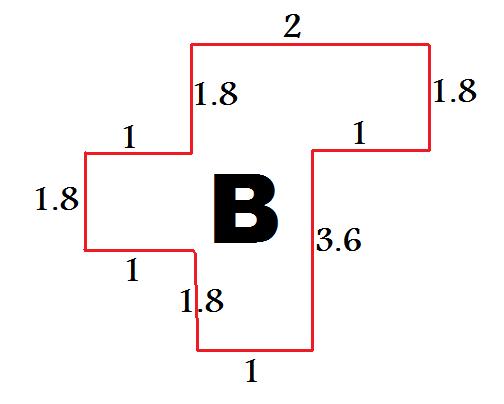
So we first stretch each country by its scale factor in the vertical direction. For example, the country B would have new dimensions as below:
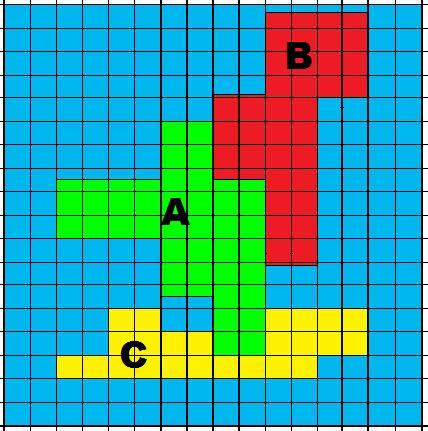
And so the overall map becomes (each square has dimensions 0.5 x 0.5)
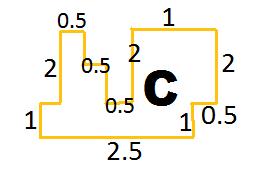
We now scale in the horizontal direction, and for example the country C (marked in yellow) would have new dimensions as below:
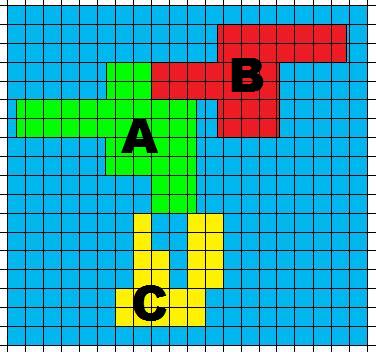
And so the overall map becomes (each square again with dimensions 0.5 x 0.5)
Now we combine the scaling factors in both the horizontal and vertical directions. For example, the country A would have dimensions as below:
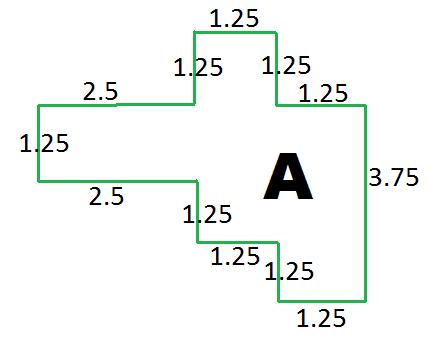
Well done to Jack from the King John School, who made a good attempt at resizing the countries in both directions. We leave this part for you to try! Perhaps scale countries B and C next, and then draw them on a map, making sure the ratio of land to ocean is kept constant.
You may also like
Golden Thoughts
Rectangle PQRS has X and Y on the edges. Triangles PQY, YRX and XSP have equal areas. Prove X and Y divide the sides of PQRS in the golden ratio.
At a Glance
The area of a regular pentagon looks about twice as a big as the pentangle star drawn within it. Is it?
Contact
A circular plate rolls in contact with the sides of a rectangular tray. How much of its circumference comes into contact with the sides of the tray when it rolls around one circuit?

