Skip over navigation
Cambridge University Faculty of Mathematics NRich logo
menu search
  • Teachers expand_more
    • Early years
    • Primary
    • Secondary
    • Post-16
    • Events
    • Professional development
  • Students expand_more
    • Primary
    • Secondary
    • Post-16
  • Parents expand_more
    • Early Years
    • Primary
    • Secondary
    • Post-16
  • Problem-Solving Schools
  • About NRICH expand_more
    • About us
    • Impact stories
    • Support us
    • Our funders
    • Contact us
  • search

Or search by topic

Number and algebra

  • The Number System and Place Value
  • Calculations and Numerical Methods
  • Fractions, Decimals, Percentages, Ratio and Proportion
  • Properties of Numbers
  • Patterns, Sequences and Structure
  • Algebraic expressions, equations and formulae
  • Coordinates, Functions and Graphs

Geometry and measure

  • Angles, Polygons, and Geometrical Proof
  • 3D Geometry, Shape and Space
  • Measuring and calculating with units
  • Transformations and constructions
  • Pythagoras and Trigonometry
  • Vectors and Matrices

Probability and statistics

  • Handling, Processing and Representing Data
  • Probability

Working mathematically

  • Thinking mathematically
  • Developing positive attitudes
  • Cross-curricular contexts

Advanced mathematics

  • Decision Mathematics and Combinatorics
  • Advanced Probability and Statistics
  • Mechanics
  • Calculus

For younger learners

  • Early Years Foundation Stage

Sizing Them Up

Age 5 to 7
Challenge Level Yellow star
Primary curriculum
  • Problem
  • Getting Started
  • Student Solutions
  • Teachers' Resources


Arrange these shapes in order of size. Put the smallest first.

How are you deciding on the order?

 

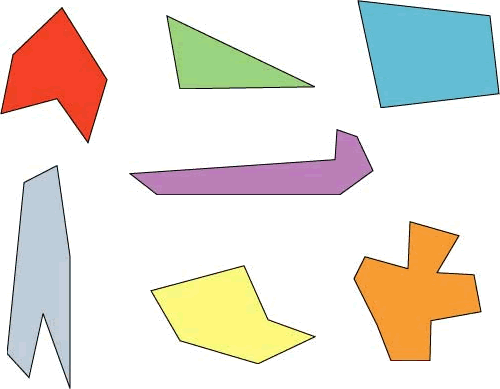
seven irregular shapes
 
 
You may like to use the interactivity below to keep track of the order and/or to record your final solution.

 

 

Once you've had a chance to think about it, click below to see how four different pupils began working on the task.

Kelsey said:

"I printed the shapes and then measured the length of each shape at the longest point." 

 

Louise and Rosie said:

"We observed the area of each and tried to rearrange the shapes in our heads to compare them." 

 

Thomas said:

"I cut out the shapes then cut each up into little pieces and laid them on top of each other to see which was bigger. I also put them on a grid with small squares and counted the number of squares for each." 


Can you take each of these starting ideas and develop it into a solution?

You may be interested in the other problems in our Celebrating Solutions Feature.

Related Collections

  • Back to LTHC resources

You may also like

Three Squares

What is the greatest number of squares you can make by overlapping three squares?

Two Dice

Find all the numbers that can be made by adding the dots on two dice.

Biscuit Decorations

Andrew decorated 20 biscuits to take to a party. He lined them up and put icing on every second biscuit and different decorations on other biscuits. How many biscuits weren't decorated?

  • Tech help
  • Accessibility Statement
  • Sign up to our newsletter
  • Twitter X logo

The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice.

NRICH is part of the family of activities in the Millennium Mathematics Project.

University of Cambridge logo NRICH logo