Skip over navigation
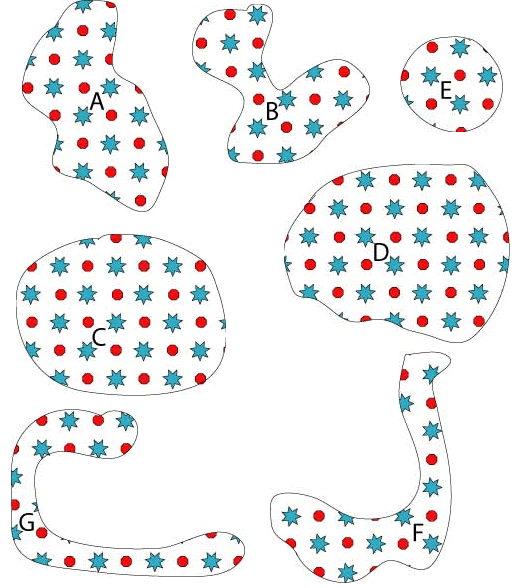
Arrange these pieces of wallpaper in order of size. Put the smallest first.
Wallpaper
Age 5 to 7
Challenge Level 
Wallpaper
Arrange these pieces of wallpaper in order of size. Put the smallest first.
Can you explain how you did it?
Why do this problem?
This activity is designed to help children begin to understand the meaning of area. It is a follow-up to Sizing Them Up and it makes an explicit link to the concept of area. The context of wallpaper or wrapping paper might be familiar to some children and therefore might hook them in and capture their curiosity.Possible approach
You could start the activity off by showing the children two of the shapes which are obviously very different "sizes" so that they will agree on an order. Invite them to explain why they ordered them in that way.
After this you could show the children the shapes from this sheet. Then they could work in pairs with the shapes. It is important to allow plenty of time for children to share their ordering and explanations
with their partners and the rest of the group.
In this challenge, pupils can use the pattern on the wallpaper to count the number of stars and/or spots inside each piece so that they should end up with the same ordering. It is likely that they will spend some time discussing how best to approach this problem before reaching that conclusion.
If they do not suggest counting the stars and spots you could say something like, "I wonder how many stars there are on this shape?". This could lead into a discussion about why it might be useful for everyone to have the same way of working out how much space is covered by an object - perhaps relating it to a sports pitch or a tablecloth.
In this challenge, pupils can use the pattern on the wallpaper to count the number of stars and/or spots inside each piece so that they should end up with the same ordering. It is likely that they will spend some time discussing how best to approach this problem before reaching that conclusion.
If they do not suggest counting the stars and spots you could say something like, "I wonder how many stars there are on this shape?". This could lead into a discussion about why it might be useful for everyone to have the same way of working out how much space is covered by an object - perhaps relating it to a sports pitch or a tablecloth.
There is no reason why you should not make your own irregular shapes from wallpaper or wrapping paper using the activity as an idea rather than a problem to be solved.
Key questions
How are you going to decide which is smallest?
How might the pattern on the wallpaper help?Possible extension
You could extend the challenge by adding in a piece of wallpaper or wrapping paper of your own which has a different pattern and ask the children to cut different shapes of the "same size".Possible support
Suggest counting the stars and spots on each shape and recording them in some way.You may also like
Biscuit Decorations
Andrew decorated 20 biscuits to take to a party. He lined them up and put icing on every second biscuit and different decorations on other biscuits. How many biscuits weren't decorated?