Skip over navigation
It is such fun to do some tessellating!
I've been using some Polydron (plastic shapes which click together) and making some rules before setting off:
Rule one - we will use six equilateral triangles for a shape and that'll be our tessellating shape.
Rule two - we can flip the shape over and turn it around but the basic shape - the way the triangles are connected - must remain the same.
Well, here's one I started with:
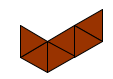
Then I tried to put a number of these together;
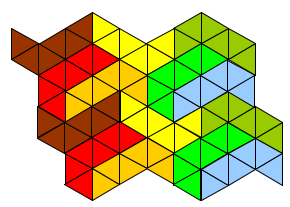
I had to flip the brown one over to get the red one, rotate it to get the blue one, and so on.
Having done this much of the tessellation, I could see that it could easily continue on for ever!
Can you find out or see why?
Then I tried another:
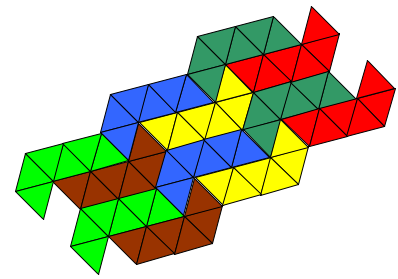
This came about by just turning the brown one around to get the greens and blue.
Do you think this one could go on and on? If so, why?
Now the third one I got was like this:
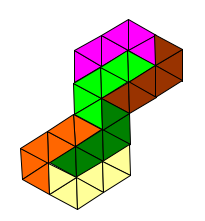
This I rather liked because it seemed to be complete and did not have anything sticking out.
I wonder if you can see what flips and turns I did with the pink one to get some of the others?
Would this one go on and on?
If so, how would you go about it?
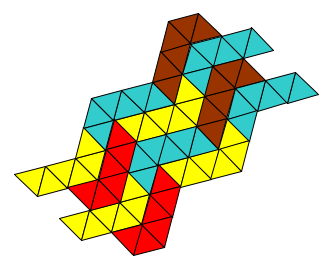
Well there's the last one I'm sharing.
What can you say about it?
Well I think it's your turn (or flip!!).
What ones can you make?
You could start with the 6 put together like mine - and maybe try to do one of those above.
OR
You could find other tessellating shapes with the same starting shape.
OR
You could design your own 6-triangle shape and start tessellating.
Tessellating Transformations
Age 7 to 11
Challenge Level 
Tessellating Transformations
It is such fun to do some tessellating!
I've been using some Polydron (plastic shapes which click together) and making some rules before setting off:
Rule one - we will use six equilateral triangles for a shape and that'll be our tessellating shape.
Rule two - we can flip the shape over and turn it around but the basic shape - the way the triangles are connected - must remain the same.
Well, here's one I started with:
Then I tried to put a number of these together;
I had to flip the brown one over to get the red one, rotate it to get the blue one, and so on.
Having done this much of the tessellation, I could see that it could easily continue on for ever!
Can you find out or see why?
Then I tried another:
This came about by just turning the brown one around to get the greens and blue.
Do you think this one could go on and on? If so, why?
Now the third one I got was like this:
This I rather liked because it seemed to be complete and did not have anything sticking out.
I wonder if you can see what flips and turns I did with the pink one to get some of the others?
Would this one go on and on?
If so, how would you go about it?
Well there's the last one I'm sharing.
What can you say about it?
Well I think it's your turn (or flip!!).
What ones can you make?
You could start with the 6 put together like mine - and maybe try to do one of those above.
OR
You could find other tessellating shapes with the same starting shape.
OR
You could design your own 6-triangle shape and start tessellating.
Why do this problem?
I cannot recommend this activity too highly; you should try it for yourself. When you do so, notice all the confusions that arise about which way up the shape should go to "fit in". These confusions provide motivation for lively discussion between pupils (where they will need to use relevant mathematical vocabulary) and a great deal of
hands-on trial and improvement.
Possible approach
Present the children with some equilateral connecting triangles. Then set them the problem showing them the examples on the site. It is also very worthwhile to look at using other basic 6-triangle shapes. Some have lots going for them and others are not so good, but this in itself is useful to talk about with pupils as they try other shapes.
Here are two to be going on with that I tried:
At some stage you may reach a definition for "tessellation" that the children come up with and find useful when deciding if a pattern is ok or not.
Key questions
Tell me about the shapes that you've made.
Possible extension
An extension would be to use two different basic shapes to tessellate with and discuss the advantages and disadvantages of doing this. At some stage you may reach a definition for "tessellation" that the children come up with and find useful when deciding if a pattern is OK or not.
Possible support
Some pupils may need help manipulating the triangles spme computer programs may be helpful.
You may also like
Penta Place
Penta people, the Pentominoes, always build their houses from five square rooms. I wonder how many different Penta homes you can create?
Tessellating Triangles
Can you make these equilateral triangles fit together to cover the paper without any gaps between them? Can you tessellate isosceles triangles?
