Skip over navigation
I've been seeing tessellations in lots of different places and realise that they are being used in so many situations such as tiling on both walls and floors.
At visits to various garages and big buildings I've seen one particular style of tile that's good to create and tessellate. Here's how it goes.
A - You start with a rectangle that is twice as long as it is wide.
B - Then you make a roof shape at one end - this one happens to be as high as a quarter of the base of the triangle it has made.
C - You then put the same triangle on the other end.
D - On one side you take a bite out just the same size as the roof triangle.
E - Then do the same at the other end of the opposite side.
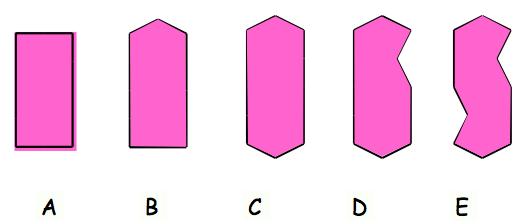
Now you have the tile shape for tessellating like the floors I've seen.
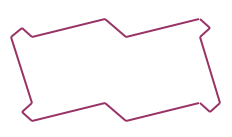
One way I've seen is like this:
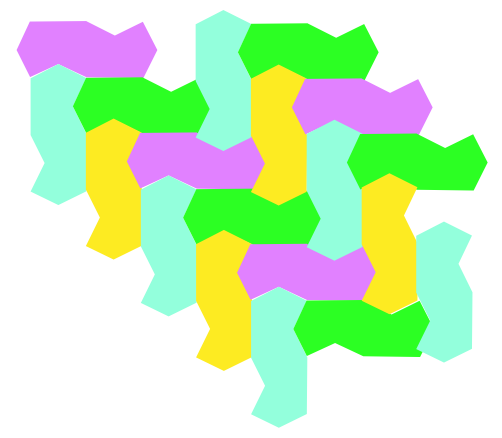
At another garage I saw a tile like this:
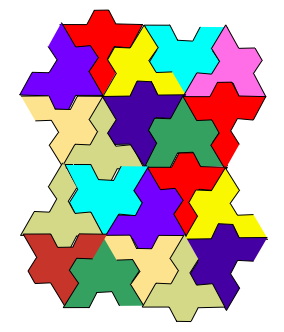
These were put together like this [I've coloured them to see the pattern more easily]:
or
Now it's time for you to try and find some ways of putting shapes - like these two examples - together!
Let us know how you made your shape and do send us some pictures of your tessellations.
You may have carried out transformations (like the first one on the rectangle) on other shapes.
A very simple idea can be explored with equilateral triangles - an Escher favourite:
These can be put together in different ways.
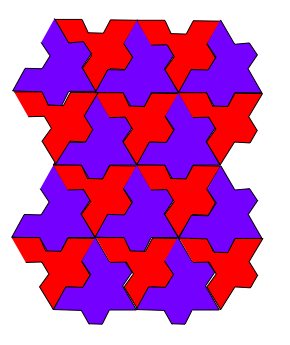
Again there's lots of opportunity for discussion with certain pupils. For example, "Is there always a need for two different kinds of the transformed triangles?"
Escher Tessellations
Age 7 to 11
Challenge Level 
Escher Tesselations
I've been seeing tessellations in lots of different places and realise that they are being used in so many situations such as tiling on both walls and floors.
At visits to various garages and big buildings I've seen one particular style of tile that's good to create and tessellate. Here's how it goes.
A - You start with a rectangle that is twice as long as it is wide.
B - Then you make a roof shape at one end - this one happens to be as high as a quarter of the base of the triangle it has made.
C - You then put the same triangle on the other end.
D - On one side you take a bite out just the same size as the roof triangle.
E - Then do the same at the other end of the opposite side.
Now you have the tile shape for tessellating like the floors I've seen.
One way I've seen is like this:
At another garage I saw a tile like this:
These were put together like this [I've coloured them to see the pattern more easily]:
or
Now it's time for you to try and find some ways of putting shapes - like these two examples - together!
Let us know how you made your shape and do send us some pictures of your tessellations.
Why do this problem?
This very practical activity creates an opportunity for investigating properties of shapes in an informal way. Asking them to tackle this in pairs or small groups will mean that talking to each other will be necessary, and this discussion can reveal a great deal to you about their knowledge and mathematical skills.Possible approach
It is important to consider what part the recording of this work plays in the development of children's concepts relating to tessellation.Key questions
Possible extension
Those of you who are Escher fans will probably have resources that can extend this activity.You may have carried out transformations (like the first one on the rectangle) on other shapes.
A very simple idea can be explored with equilateral triangles - an Escher favourite:
These can be put together in different ways.
Again there's lots of opportunity for discussion with certain pupils. For example, "Is there always a need for two different kinds of the transformed triangles?"
Possible support
You may also like
Penta Place
Penta people, the Pentominoes, always build their houses from five square rooms. I wonder how many different Penta homes you can create?
Tessellating Triangles
Can you make these equilateral triangles fit together to cover the paper without any gaps between them? Can you tessellate isosceles triangles?
