Skip over navigation
I know that when doing symmetry we often have a look at CAPITAL LETTERS.
We could try tessellating certain ones, deciding on good ones to try and those that would be no good.
A simple one to start with is the letter C - see what has happened when I've tried to tessellate them:
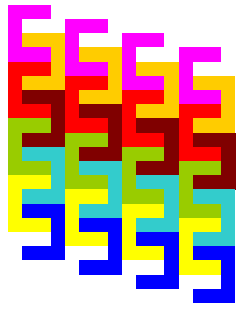
Not hard!
Slightly different we have:
Do you see how they are different?
Now try another one or two for yourself!
Capital F also seems a good one, but maybe it's a little harder.
I must admit I chose the sizes to be a bit easier!
I decided to lay two of them down like this:
Then playing about with putting them together I got:
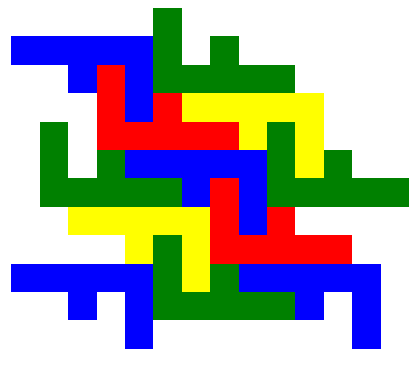
This I was quite happy with, so I thought that having shown you, you could try some for yourself.
Please send us your tessellations. You could scan a drawing into the computer and send it that way, or you might like to take a digital photo of the tessellations.
The problem is good for developing pupils' ability to visualise, and depending on their experience, you may also want to use this as an opportunity to encourage them to use correct mathematical vocabulary relating to transformations.
Other simple C's I found were;
and
Just to carry on here is an H tessellation.
It's also good to look at what seem like very simple [maybe too simple, we think!] letters and find many ways of tessellating them. To show you the sort of thing I mean look at these variations on tessellating the simple letter L. I used four different orientations and coloured them to help.
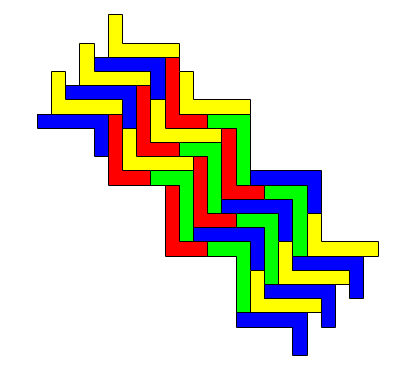
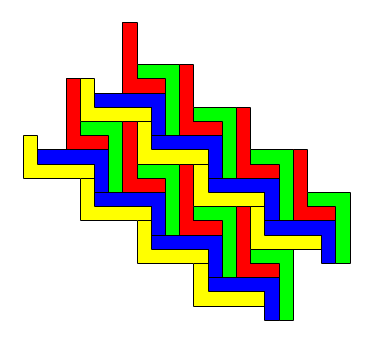
Could this tessellation be continued for ever? Why or why not?
What is the single repeating unit in the tessellation?
How would you describe the tessellation to someone else?
Tessellating Capitals
Age 5 to 7
Challenge Level 
Tesselating Capitals
I know that when doing symmetry we often have a look at CAPITAL LETTERS.
We could try tessellating certain ones, deciding on good ones to try and those that would be no good.
A simple one to start with is the letter C - see what has happened when I've tried to tessellate them:
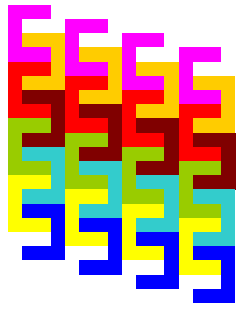
Not hard!
Slightly different we have:
Do you see how they are different?
Now try another one or two for yourself!
Capital F also seems a good one, but maybe it's a little harder.
I must admit I chose the sizes to be a bit easier!
I decided to lay two of them down like this:
Then playing about with putting them together I got:
This I was quite happy with, so I thought that having shown you, you could try some for yourself.
Please send us your tessellations. You could scan a drawing into the computer and send it that way, or you might like to take a digital photo of the tessellations.
Why do this problem?
This is a really good activity to engage all children. Those who are less motivated and find mathematics difficult will be able to have a go (and may well surprise you) but there is also enjoyment and intrigue here for the enthusiastic and mature mathematician!The problem is good for developing pupils' ability to visualise, and depending on their experience, you may also want to use this as an opportunity to encourage them to use correct mathematical vocabulary relating to transformations.
Possible approach
This is a sheet with four letters, though you could use other ones too.Other simple C's I found were;
and
Just to carry on here is an H tessellation.
It's also good to look at what seem like very simple [maybe too simple, we think!] letters and find many ways of tessellating them. To show you the sort of thing I mean look at these variations on tessellating the simple letter L. I used four different orientations and coloured them to help.
Key questions
The following questions might be useful in coaxing children to think more deeply, and perhaps differently, about what they are doing:Could this tessellation be continued for ever? Why or why not?
What is the single repeating unit in the tessellation?
How would you describe the tessellation to someone else?