Skip over navigation
Answer: 7
Using expressions
Let the number of Boys in Group 1 be $x$.
The number of Girls in Group 1 is therefore $40-x$.
Therefore the number of Girls in Group 2 is $33 - (40 - x) = x - 7$.
There are therefore $7$ more Boys in Group 1 than Girls in Group 2.
Using an example
If all the Boys are in Group 1 there will be:
If we swap one Boy from Group 1 with one Girl from Group 2 there will be:
If we continue in the same way, as the number of Boys in Group 1 goes down by 1, the number of Girls in Group 2 will also go down by 1, so the difference will always be 7.
Using a table
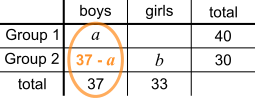
$$\begin{align}30-b&=37-a\\
-b+a&=37-30\\
a-b&=7\end{align}$$
Forming Groups
Age 11 to 14
ShortChallenge Level 
Answer: 7
Using expressions
Let the number of Boys in Group 1 be $x$.
The number of Girls in Group 1 is therefore $40-x$.
Therefore the number of Girls in Group 2 is $33 - (40 - x) = x - 7$.
There are therefore $7$ more Boys in Group 1 than Girls in Group 2.
Using an example
If all the Boys are in Group 1 there will be:
37 Boys and 3 Girls in Group 1
30 Girls in Group 2
If we swap one Boy from Group 1 with one Girl from Group 2 there will be:
36 Boys and 4 Girls in Group 1
29 Girls and 1 Boy in Group 2
29 Girls and 1 Boy in Group 2
If we continue in the same way, as the number of Boys in Group 1 goes down by 1, the number of Girls in Group 2 will also go down by 1, so the difference will always be 7.
Using a table
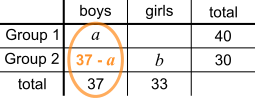
$$\begin{align}30-b&=37-a\\
-b+a&=37-30\\
a-b&=7\end{align}$$
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Long Shadows
Weekly Problem 10 - 2012
If you know how long Meg's shadow is, can you work out how long the shadow is when she stands on her brother's shoulders?
Ice Cream Pie
The pie chart shows the different types of ice creams on sale. How many chocolate ice creams were sold?