Skip over navigation
Answer: 9 (so the number is 12349678)
Using division
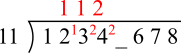
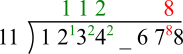
The number is divisible by 11 so there must have been a remainder of 8 to give 88
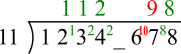
___7 gives a remainder of 8
107 = 99 + 8
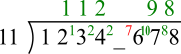
___6 gives a remainder of 10
Using place value and algebra
Missing Digit
Age 11 to 14
ShortChallenge Level 
Answer: 9 (so the number is 12349678)
Using division
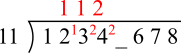
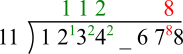
The number is divisible by 11 so there must have been a remainder of 8 to give 88
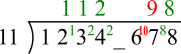
___7 gives a remainder of 8
107 = 99 + 8
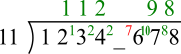
___6 gives a remainder of 10
76 = 66 + 10
2__ gives a remainder of 7
22 + 7 = 29
9 is missing
Using a divisibility test
A test for divisibility by 11 is to add alternate digits:
2__ gives a remainder of 7
22 + 7 = 29
9 is missing
Using a divisibility test
A test for divisibility by 11 is to add alternate digits:
1 + 3 + * + 7 = 11 + *; 2 + 4 + 6 + 8 = 20.
If the original number is a multiple of 11 then these two totals will be the same or will differ by a multiple of 11. In this case, 11 + * = 20 gives * = 9.
Using place value and algebra
1234*678 = 12340678 + 1000* = (11 x 1121879 +9) + 11 x 90* + 10*
and hence is divisible by 11 if and only if 10* + 9 is divisible by 11. So * = 9.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Adding All Nine
Make a set of numbers that use all the digits from 1 to 9, once and once only. Add them up. The result is divisible by 9. Add each of the digits in the new number. What is their sum? Now try some other possibilities for yourself!
Repeaters
Choose any 3 digits and make a 6 digit number by repeating the 3 digits in the same order (e.g. 594594). Explain why whatever digits you choose the number will always be divisible by 7, 11 and 13.