Skip over navigation

Sticks and Triangles

Age 7 to 11

Challenge Level Yellow star

Sticks and Triangles

I made some triangles out of sticks. The sticks are all the same length.

I can make a triangle out of three sticks:

What about four sticks? Five sticks? Six sticks?

I can make two different triangles out of ten sticks:

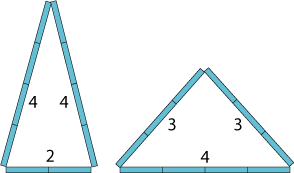
Can you find any others?

What about triangles made from twenty sticks?

What about all the lengths in between?

Can you make any rules about the numbers of sticks that make the most triangles?

Why do this problem?

This problem is one where learners have to work systematically, and find a way to record, organise and explain their findings, making sure they have found all possibilities. While doing this, they will also come across some interesting facts about the shapes of triangles and patterns in numbers.

The problem can be done by drawing, but is easier, and more revealing using sticks. These can be headless matchsticks, drinking straws cut into equal lengths, lolly sticks or even new pencils if you have the pencils and the space!

Possible approach

You could start by showing the problem as it is given from a computer or print out of the text. Alternatively, you could hand out sticks and ask the group what is the least number of sticks they will need to make a triangle. Then ask them to see if they can make a triangle with four sticks. It might be a good idea at this point to make quite sure that all the group know that a triangle has three straight sides!

Next, it might be appropriate for the group to make a hypothesis regarding which numbers of sticks will make the most triangles prior to actually working on the problem. This will help give a focus for follow-up discussion.

After this, learners could work in pairs on the problem so that they are able to talk through their ideas with a partner. They should be encouraged to record the various findings in some way.

At the end there should be time to discuss their findings. Ask them for which numbers of sticks did they find the most triangles? Can they think why this should be so?

Things to draw out from this activity include:

* differences between odd and even numbers of sticks.

* looking at numbers of sticks which are multiples of three.

* any "rules" for when it is possible to construct a triangle and when it isn't.

* looking at different ways that findings could be recorded.

* making suggestions of ways that the enquiry could be extended.

Key questions

How are you going to record your findings?
Are you sure you have found all the possible triangles with that number of sticks?
Whatever number of sticks you are trying, it would it be a good idea to start by trying to make a triangle which has just one stick as a side.
How many sticks have you along the base of that triangle?
Could you try another number of sticks along the base?
Can you see any differences between odd and even numbers of sticks?
What about looking at numbers of sticks which are multiples of three?

Possible support

Suggest that learners who find this problem difficult work steadily with real sticks starting with triangles with three sticks and working upwards. Drawing what they have done is probably the easiest way to record but it might be helpful to show them how a table can be made of their results. It may be helpful for children to have had a go at the task Let's Investigate Triangles as a precursor to this one.

Possible extension

Learners could make a table of results and formulate any 'rules' for when it is possible to construct a triangle and when it is not possible. They could then predict the numbers of triangles they should be able to make for 21 to 30 sticks and then test their predictions.

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Sticks and Triangles

Sticks and Triangles

Why do this problem?

Possible approach

Key questions

Possible support

Possible extension

You may also like

Geoboards

Polydron

Multilink Cubes