Numbers as Shapes

Here are the numbers $1$ to $6$ drawn using coloured squares:

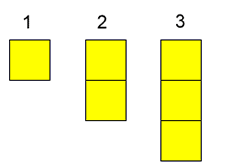
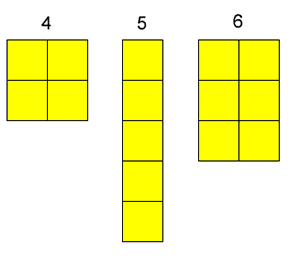
We can call these numbers squares, rectangles or sticks.

$1$ is a square but just a single one.
We can't make $2$ into a square so $2$ is a stick.
We can't make $3$ into a square or a rectangle so $3$ can only be a stick.
We can make $4$ into a square.
We can't make $5$ into a square or a rectangle, so $5$ can only be a stick.
We can't make $6$ into a square, but we can make $6$ into a rectangle.

If you had $7$ yellow squares, what could you make them into? A square, a rectangle or a stick? How about $8$ squares?

Try this with the numbers up to and including $20$.

Which ones can only be sticks?
Which ones can make rectangles?
Which ones are squares?

What do you notice?

This problem was inspired by a session at an ATM conference, led by Tandi Clausen-May.