Oranges and Lemons, Say the Bells of St Clement's

Bellringers have a special way to write down the patterns in which their bells are rung. They give each bell a number, starting with the bell with the highest pitch at number 1 and working down so that the bell with the lowest pitch has the largest number. They write down their patterns in rows. Each row is read from left to right, and the rows are read from top to bottom.

Change ringing requires each bell to be played exactly once in each row. To move from one row to the next, we swap round some of the bells. We can only swap two bells if they are next to each other (although we can swap several pairs at a time).

Here is an example of a pattern for four bells.

1234

2143

2413

4231

4321

3412

3142

1324

1234

Can you see which bells are swapped at each stage? You might find it useful to write down the positions of any bells that don't move in between two rows.

Hopefully you have seen that on alternate rows we swap all of the bells (in pairs, of course - and there is only one way to do this). On the remaining rows, we fix the bells on either end and swap the rest. We repeat this until we get back to the starting pattern (1234), which happens after 8 changes.

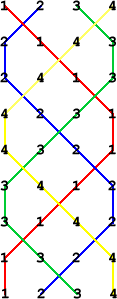
We can add coloured lines to show the paths of the different bells. This is how bellringers remember what to do.

Now let's try the same pattern with six bells. (That is, swap all the bells in pairs, then fix the end two and swap the rest in pairs, then swap all the bells, then fix the end two and swap the rest in pairs, etc.) How many changes does it take to get back to 123456? Write out the rows.

Draw on the paths of the different bells.You might need some coloured pencils!

Can you draw the pattern for eight bells without writing out the numbers?