All about Ratios

Excellent solutions were sent in by Michael from Wilmslow High School, Cheshire, UK and Andrei from Tudor Vianu National College, Bucharest, Romania.

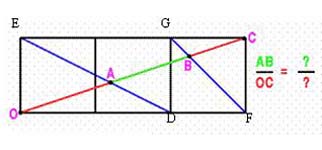(1) As triangles AOD and AEC are similar $${OA\over AC} = {OD\over EC} = {2\over 3} {\Rightarrow}{OA\over OC} = {2\over 5}.$$ As triangles BOF and BCG are similar $${OB\over BC} = {OF\over GC} = {3\over 1} {\Rightarrow} {OB\over OC} = {3\over 4}.$$ Hence: $${AB\over OC} = {OB - OA\over OC} = {3\over 4} - {2\over 5} = {7\over 20}.$$

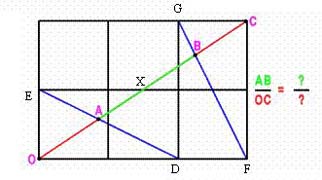(2) From triangles OAD and AXE $${OA\over AX} = {OD\over EX} = {2\over 1.5}= {4\over 3}$$ and hence $${OA\over OX} = {4\over 7} \quad {\rm and} \quad {OA\over OC} = {2\over 7}.$$ Again $${OB\over OC} = {3\over 4}.$$ Hence: $${AB\over OC} = {OB - OA\over OC} = {3\over 4} - {2\over 7} = {13\over 28}.$$

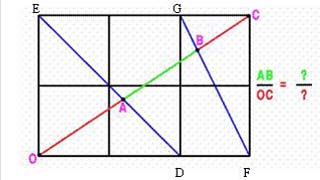(3) The reasoning in this part is identical to part (1).