Triangle Numbers

Well done Amelia and Kahlia from Ardingly College, Lauren from St. Matthew's School and Kate from Orston Primary for realising that the pattern would continue indefinitely.

Kahlia reminded us that

"Triangle numbers are numbers which can form a triangle."

$1$
$1 + 2$
$1 + 2 + 3$
$1 + 2 + 3 + 4 $
$1 + 2 + 3 + 4 + 5 $
$1 + 2 + 3 + 4 + 5 + 6 $
$1 + 2 + 3 + 4 + 5 + 6 + 7$

we add an even number, then an odd number, then another even number, then another odd number, and so on.

Lauren noticed that:

"All the odd numbers along the top e.g. $1, 3, 5, 7, 9, 11$ have a couple of triangle numbers underneath."

And Kate noticed that:

"The difference between the two triangular numbers above and below each other on the table square is the same as the number at the top.
e.g. the difference between $3$ and $6$ is three, which is above them on the square."

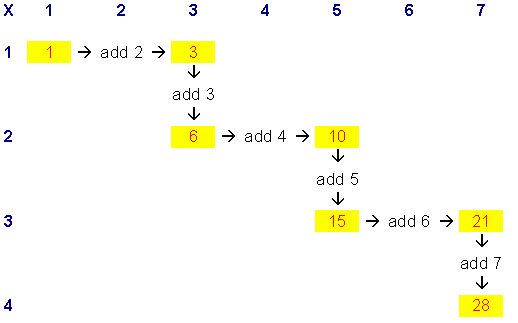
So that clarifies why we go down from one triangle number to another along odd numbered columns when the difference between the triangle numbers is odd.

On each row we move two squares across, so that takes care of having to add the next even number:
Moving two squares across on the first row adds $2$
Moving two squares across on the second row adds $4$
Moving two squares across on the third row adds $6$
And so on.

So, moving across adds the next even number, moving down adds the next odd number:

Paul offered another way to think about it: