Skip over navigation
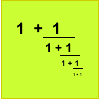
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Not Continued Fractions
Age 14 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
- The key here is that $x$ has to be the integer part of $N$ because the 'continued fraction' part of the expression gives a value less than one.
As $y$ and $z$ are positive integers (whole numbers), $y + 1/z > 1$ and $1/(y+1/z) < 1$ so we know that this must equal $3/7$ and $x = 1$.
Hence $y + 1/z = 7/3$. Again $y$ has to be the integer part of $7/3$ so $y = 2$ and $z = 3$.
- As in the first part, if $N = 8/5$, then we must have $x = 1$ and $y + 1/z = 5/3$.
To make $y$ and $z$ positive integers we must have $1/z < 1$ and $y = 1$.
It then follows that $1/z = 2/3$ so it is impossible to find positive integer values for $x$, $y$ and $z$.
You may also like
Good Approximations
Solve quadratic equations and use continued fractions to find rational approximations to irrational numbers.
There's a Limit
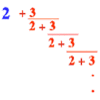
Explore the continued fraction: 2+3/(2+3/(2+3/2+...)) What do you notice when successive terms are taken? What happens to the terms if the fraction goes on indefinitely?

