Resistance

What is infinity plus one? This may be a sufficient hint to help you solve the problem. Have a go before reading any further.

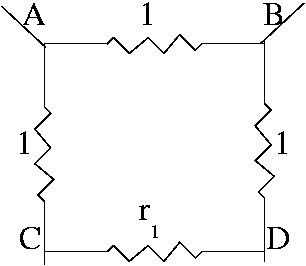
One approach to solving problems involving an infinite system like this one is to focus on the idea of infinity and its properties. Removing one item from an infinite system does not change the value for the whole system. This idea is the key to the simplest method of solving this particular problem. In this diagram the infinite ladder extends downwards and the network below C and D is effectively the same as the network below A and B. The total resistance $r_1$ between C and D, for the infinite network, will be the same as the total resistance $R$ between A and B. So we can think of the resistance between A and B as a resistance of 1 ohm in parallel with three resistances in series. Write down the equation and you will get a simple quadratic equation to solve for $R$.

An alternative method is to start with simple cases. When we have an infinite system we often start with $n=1$ and 2, 3, ... and try to find a formula for $n$ and then calculate its limit as ${n\to \infty}$. Very often this method of solving a problem is the best one but not always. In this case the method leads to an infinite continued fraction which can be evaluated to give the required value of the resistance.