Skip over navigation
Cambridge University Faculty of Mathematics NRich logo
menu search
  • Teachers expand_more
    • Early years
    • Primary
    • Secondary
    • Post-16
    • Events
    • Professional development
  • Students expand_more
    • Primary
    • Secondary
    • Post-16
  • Parents expand_more
    • Early Years
    • Primary
    • Secondary
    • Post-16
  • Problem-Solving Schools
  • About NRICH expand_more
    • About us
    • Impact stories
    • Support us
    • Our funders
    • Contact us
  • search

Or search by topic

Number and algebra

  • The Number System and Place Value
  • Calculations and Numerical Methods
  • Fractions, Decimals, Percentages, Ratio and Proportion
  • Properties of Numbers
  • Patterns, Sequences and Structure
  • Algebraic expressions, equations and formulae
  • Coordinates, Functions and Graphs

Geometry and measure

  • Angles, Polygons, and Geometrical Proof
  • 3D Geometry, Shape and Space
  • Measuring and calculating with units
  • Transformations and constructions
  • Pythagoras and Trigonometry
  • Vectors and Matrices

Probability and statistics

  • Handling, Processing and Representing Data
  • Probability

Working mathematically

  • Thinking mathematically
  • Developing positive attitudes
  • Cross-curricular contexts

Advanced mathematics

  • Decision Mathematics and Combinatorics
  • Advanced Probability and Statistics
  • Mechanics
  • Calculus

For younger learners

  • Early Years Foundation Stage

Twice as Big?

Age 7 to 11
Challenge Level Yellow star
Primary curriculum
  • Problem
  • Getting Started
  • Student Solutions
  • Teachers' Resources

Twice as Big?


If we double each side of a small square we get a new enlarged square:

 

 

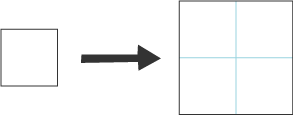
square to square with sides twice as long

 


The new enlarged square is the size of four of the smaller squares.

This also happens when we enlarge other shapes. Some, like the squares, can be filled with the same smaller shape.

Look at these:



Can you work out how the four shapes fit to make the enlarged shape each time?
You need to rotate or reflect the smaller shapes to fit them in. (This means that if you make them from squared paper you will need to turn them round or turn them over.)

Please send us pictures of your completed shapes.

In this interactivity the rotation and the reflection of the shapes has been done for you.

If you enjoyed working on this problem, you might like to investigate some more shapes. Have a look at Two Squared or print out this sheet which contains some other examples as well as the shapes above.

 

Why do this problem?

 

This problem encourages children to use visualisation and will help to improve their spatial awareness.

 

Although, as it stands, the problem focuses on fitting the shapes into their enlarged version, it makes a good stepping stone to discussing what "bigger" means. Ask the class to investigate the difference in perimeter and area of the small and large version of the shapes. What do they notice?

 

 

Possible approach

 

You may like to talk to the group about some good ways to approach the problem - ask for their ideas and model some behaviours. You could place two shapes into the larger one leaving a small space which could not be filled to draw their attention to something to avoid!

 

If you are not using the interactivity, you may like to print off this sheet and cut out the shapes for the children. (The sheet also contains some shapes based on triangles as well as squares.) You may find that if they are working from "concrete" examples, the class will need reminding that they can flip and rotate the shapes.

 

 

Key questions

 

Can you think of a good way to start on this?
Why don't you try putting one shape in at a time?
Are you being careful not to leave any gaps which you won't be able to fill?
Have you remembered you can flip and rotate the shapes?

 

Possible extension

 

Learners could do the examples on the second page of this sheet or try Two Squared.

 

Possible support

Suggest using the interactivity workingon one shape at a time from the top.
 

 

You may also like

Cutting Corners

Can you make the most extraordinary, the most amazing, the most unusual patterns/designs from these triangles which are made in a special way?

Cut and Make

Cut a square of paper into three pieces as shown. Now,can you use the 3 pieces to make a large triangle, a parallelogram and the square again?

Square to L

Find a way to cut a 4 by 4 square into only two pieces, then rejoin the two pieces to make an L shape 6 units high.

  • Tech help
  • Accessibility Statement
  • Sign up to our newsletter
  • Twitter X logo

The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice.

NRICH is part of the family of activities in the Millennium Mathematics Project.

University of Cambridge logo NRICH logo