Skip over navigation
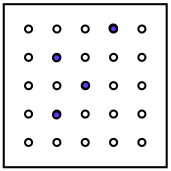
Here we have a kind of peg board. The holes go all the way through so the pegs may be seen from the top or underneath.
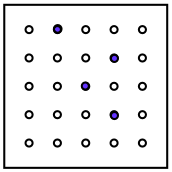
You'll see the 4 blue pegs.
Now the peg board is either:
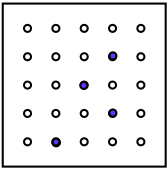
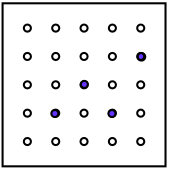
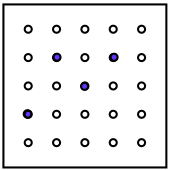
You could make some of your own and get your friends to see if they can find how you've moved it to make your next picture.

How has it been moved to show these views?

Hope you've had fun exploring these.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Peg Rotation
Age 7 to 11
Challenge Level 





Here we have a kind of peg board. The holes go all the way through so the pegs may be seen from the top or underneath.

You'll see the 4 blue pegs.
Now the peg board is either:
- flipped over - north to south, OR east to west, OR north-east to south-west, OR north-west to south-east;
- or it is rotated clockwise or anticlockwise.
Can you find out which movements could produce the four next views?




You could make some of your own and get your friends to see if they can find how you've moved it to make your next picture.
Try now to put 4 pegs in so that when you do a move with the board it still looks the same.
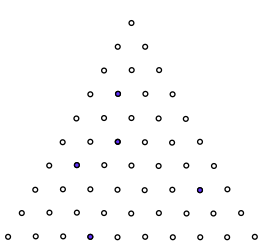
Now I've made a triangular board to do the same things.
Here's the starting view:

How has it been moved to show these views?


Hope you've had fun exploring these.
Can you think up ways of changing what I've done so that you can explore further?
You may also like
Little Boxes
How many different cuboids can you make when you use four CDs or DVDs? How about using five, then six?

