Growing Garlic

Well done to everybody who worked out that Ben planted 61 cloves of garlic. The solutions below explain different ways of working this out.

Dana from Twyford School in the UK went down from 100, checking the different possibilities for 3, 4, 5 and 6 rows until she found a number that worked in each case. She said:

I found the highest multiple of three that was under 100 which was 99 and then I added one onto that as there is always 1 left. This made 100. Then I did this for the rest of the multiples of 3. I did this for 4 rows which was 96 so I added one onto that and I had 97. Then I did it for 5 and 6 rows and when I had done this I noticed that 61 garlic cloves was on the list for 3,4,5 and 6. This is how I found out that Ben has 61 garlic cloves.

With 3 rows you can have:
100 garlics
97 garlics
94 garlics
91 garlics
88 garlics
85 garlics
82 garlics
79 garlics
76 garlics
73 garlics
70 garlics
67 garlics
64 garlics
61 garlics

With 4 rows he can have:
97 garlics
93 garlics
89 garlics
85 garlics
81 garlics
77 garlics
73 garlics
69 garlics
65 garlics
61 garlics

With 5 rows he can have:
96 garlics
91 garlics
86 garlics
81 garlics
76 garlics
71 garlics
66 garlics
61 garlics

With 6 rows he can have:
97 garlics
91 garlics
85 garlics
79 garlics
73 garlics
67 garlics
61 garlics

Ben has 61 garlic cloves altogether.

Well done Dana!

Dev from Dragon School in the UK also looked for a number that was one more than a multiple of 2, 3, 4, 5 and 6. They said:

The points I know

1) The number is less than 100

2) The total number of cloves is going to be odd because when you plant it in rows of 2, one is left over, which tells us the total number of cloves = even number + 1

3) This means total number of cloves = (multiple of 2,3,4,5,6) + 1

4) The number which is a multiple of 2,3,4,5 and 6 has to end in a 0 because it is an even number and multiple of 5

5) The even number which fits all the above conditions is 60

6) 60 is a multiple of 2,3,4,5 and 6

7) Total number of cloves Ben planted was 60+1=61

Well done for narrowing down the different possibilities, Dev. This question becomes easier when you think about finding a number which is a multiple of 2, 3, 4, 5 and 6, and then adding one to that number, so well done for spotting that method!

Ethan from Churchfields also thought about the possible ones digit of the number. He said:

If a number is one more than a multiple of 5 it has to end in a 1 or a 6. If the number ended in 6 it would be even so there would be none left over when they were planted in rows of 2.

I took all the two digit numbers below 100 that end in 1 (1 is too small) and crossed out the ones that were multiples of 3, or would have a remainder of 2 when divided by 3.

This left me with 31, 61 and 91. I then worked out what would happen if I divided them by 4. The only one with a remainder of 1 was 61 so that must be the answer.

Good work, Ethan - this is a really quick method as there aren't many numbers below 100 that end in 1. 

Dhruv from St Anne’s RC Primary School in the UK used a combination of Dev and Ethan's ideas. He sent in this explanation:

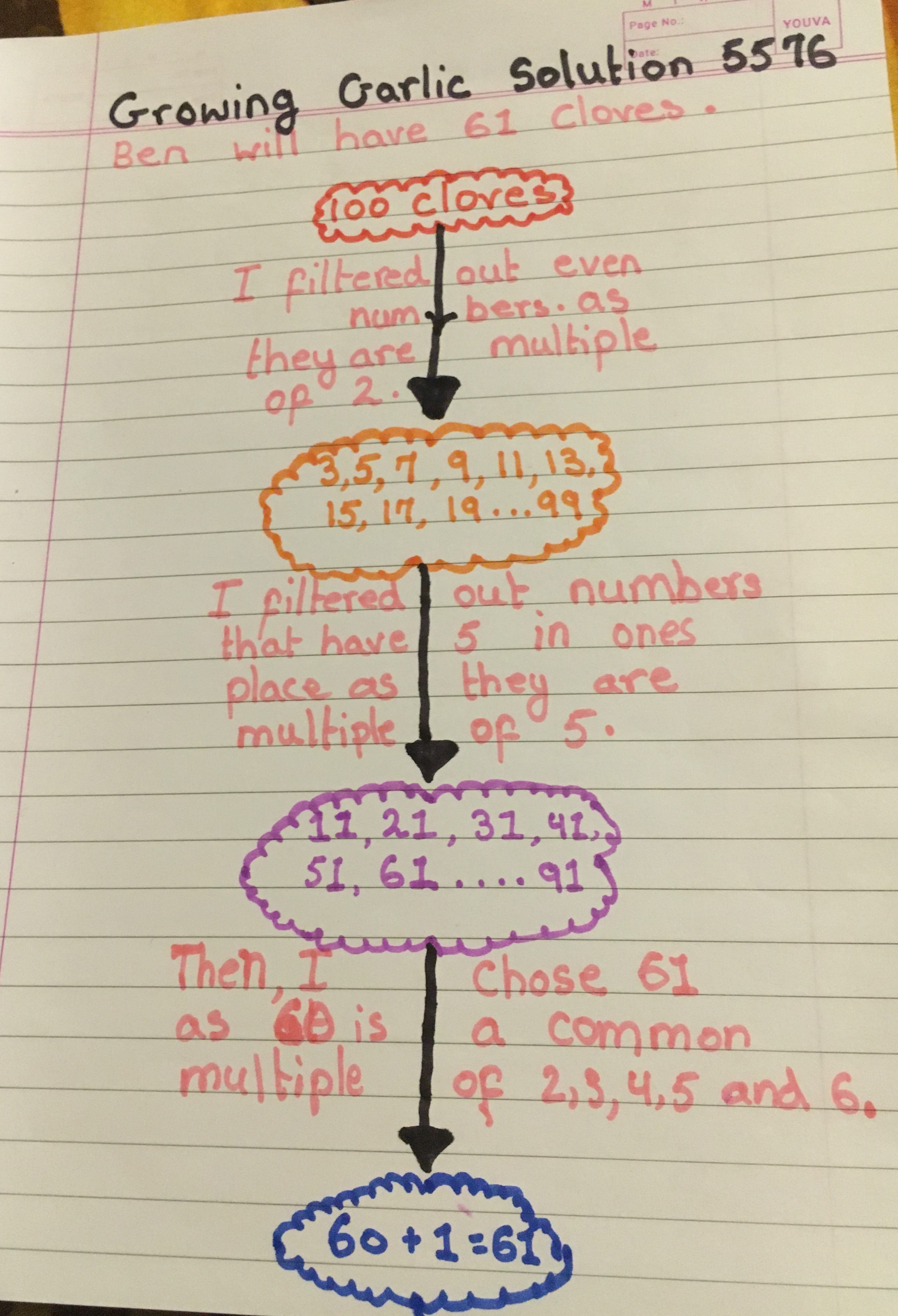
Well done Dhruv!

Arjun from Nascot Wood Junior School in the UK also used the fact that 60 is a common multiple of 2, 3, 4, 5 and 6. He said:

Since there must be 1 garlic clove left after the cloves have been sorted into 2, 3, 4, 5 and 6 rows, we must find the Lowest Common Multiple (LCM) of 2, 3, 4, 5 and 6, then add 1. You will find that the LCM is 60. 60 + 1 = 61. So the lowest amount of cloves that he can have is 61.

For above 100, the lowest multiple of 60 that is above 100 is 2 x 60 = 120. But we have to add 1, so the lowest amount of cloves that is above 100 is 121.

Good work, Arjun. I wonder what other possible amounts of cloves Ben might have had if there were more than 100?

We were also sent some good solutions by Ivan and Kenny at Sahuaro Elementary in the USA, and by Luca and Toby at Pierrepont Gamston Primary School in England. Thank you all for sending us your thoughts about this task.