Skip over navigation
This problem forms the first part of an investigation into how to represent numbers using geometric transformations that will ultimately lead us to discover numbers that are not on the number line.
I'm going to assume that you are happy with the idea of numbers that lie on the number line. Just to remind you, here is a picture of a small part of the number line.
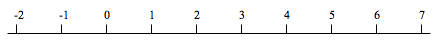
The plan of action is to develop pictures or geometric representations of the numbers we know about already. We'll also develop ways to add, subtract, multiply and divide using just those pictures. Then we'll change the picture very slightly...
Here's my first attempt at a picture of the number 1. It's simply a blue arrow.
I don't think this is a good enough picture yet, but it's helpful to think about its shortcomings.
Let's try to do arithmetic with these arrows. Try three simple additions.
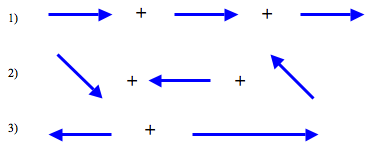
I tried these with three friends and here are the answers they gave me
Arrow Arithmetic 1
Age 14 to 16
Challenge Level 
This problem forms the first part of an investigation into how to represent numbers using geometric transformations that will ultimately lead us to discover numbers that are not on the number line.
I'm going to assume that you are happy with the idea of numbers that lie on the number line. Just to remind you, here is a picture of a small part of the number line.
The plan of action is to develop pictures or geometric representations of the numbers we know about already. We'll also develop ways to add, subtract, multiply and divide using just those pictures. Then we'll change the picture very slightly...
Here's my first attempt at a picture of the number 1. It's simply a blue arrow.
I don't think this is a good enough picture yet, but it's helpful to think about its shortcomings.
Let's try to do arithmetic with these arrows. Try three simple additions.
I tried these with three friends and here are the answers they gave me
| Sam | Hannah | Tim | |
| 1) | 3 | 3 | 3 |
| 2) | -1 | 3 | 3 |
| 3) | 1 | 3 | 2 |
They all had good explanations for their answers. Can you
guess what they were?
My arrow picture obviously has some shortcomings! How would
you improve it?
You may also like
A Story about Absolutely Nothing
This article for the young and old talks about the origins of our number system and the important role zero has to play in it.
Balance Power
Using balancing scales what is the least number of weights needed to weigh all integer masses from 1 to 1000? Placing some of the weights in the same pan as the object how many are needed?
