Skip over navigation
Here are five clowns' faces:
The clowns are called Andy, Bandy, Candy, Dandy and Eggy. The clowns do their circus acts in pairs.
Sometimes Andy and Candy work together:
What is the same about their faces? What is different?
Sometimes Andy works with Bandy:
What is the same about their faces and what is different?
Sometimes Andy works with Dandy:
What is the same about their faces? What is different?
Sometimes Bandy and Candy work together:
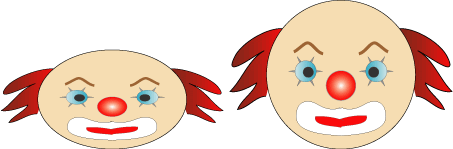
What is the same about their faces and what is different?
Sometimes Bandy works with Dandy:
What is the same about their faces? What is different?
Sometimes Candy works with Dandy:
What is the same about their faces and what is different?
Sometimes Andy works with Eggy:
What is the same about their faces? What is different?
Scaling Clowns
Age 5 to 7
Challenge Level 
Scaling Clowns
Here are five clowns' faces:
The clowns are called Andy, Bandy, Candy, Dandy and Eggy. The clowns do their circus acts in pairs.
Sometimes Andy and Candy work together:
What is the same about their faces? What is different?
Sometimes Andy works with Bandy:
What is the same about their faces and what is different?
Sometimes Andy works with Dandy:
What is the same about their faces? What is different?
Sometimes Bandy and Candy work together:
What is the same about their faces and what is different?
Sometimes Bandy works with Dandy:
What is the same about their faces? What is different?
Sometimes Candy works with Dandy:
What is the same about their faces and what is different?
Sometimes Andy works with Eggy:
What is the same about their faces? What is different?
Why do this problem?
This problem is designed to get children talking about sameness and difference in the context of size and shape. It is a good chance for them to bring familiar words into the mathematics classroom, and refine them as appropriate.Possible approach
You could start with all the group sitting on the carpet and introduce the problem as it is on the computer. This very simple interactivity is designed to be used by you, rather than individual children, so that two of the clown's faces can be easily compared by putting them into the "boxes".
It is often more difficult to point out things that have not changed and you might need to ask questions to prompt the children. You could ask them to count some features on the clowns' faces, for example. It is likely that children will use comparative words such as larger, bigger, smaller, wider, narrower, higher, shorter ... They might talk about some of the faces looking as if they have
been stretched. Depending on the children's experience, you can encourage them to be as specific as you think appropriate.
After this introduction, the group could work in pairs on the problem so that they are able to talk with a partner. These cards of the clowns' faces can be printed out and possibly laminated, and this black and white sheet of the clowns' faces can be photocopied. This sheet of 16 words related to the problem might also be useful. The children could be
challenged to draw some houses (or anything else you or they might choose!) which are big and small, wide and narrow, low and high, the same and different.
At the end of the lesson the group could show and talk about any pictures they have drawn. You could also use the interactivity again to reinforce any vocabulary the children have learnt and used.
Key questions
Can you say anything about the size of the clowns' faces?
What do you notice about the clowns' eyes?
What can you tell me about their hair/noses/mouths?
Tell me about the pictures you have drawn.
What is the difference between this picture and this picture?
Possible extension
Learners who found this problem straightforward could try this drawing problem, Scale Draw.Possible support
You could use these cards and encourage the child to talk about the differences.You may also like
Poly Plug Pattern
Create a pattern on the small grid. How could you extend your pattern on the larger grid?