Skip over navigation
One of my regular trips to Liverpool last summer took me to the Walker Art Gallery. A wonderful place with some beautiful pictures.
On my way out I stopped to browse in the small shop and discovered this toy for 50p.
What a bargain and so many questions for you to think about.
Basically the toy has the three wheels with cogs along their circumference - the smallest is pink, the middle one blue and the largest yellow. It also has two circles (I have labelled them A and B in the picture). Circle A is smaller than circle B.
Like a Circle in a Spiral
Age 7 to 16
Challenge Level 
One of my regular trips to Liverpool last summer took me to the Walker Art Gallery. A wonderful place with some beautiful pictures.
On my way out I stopped to browse in the small shop and discovered this toy for 50p.
What a bargain and so many questions for you to think about.
Basically the toy has the three wheels with cogs along their circumference - the smallest is pink, the middle one blue and the largest yellow. It also has two circles (I have labelled them A and B in the picture). Circle A is smaller than circle B.
| You need a pen or sharp pencil and lots of paper to practise with. You take a wheel and place it inside one of the two circles so that the two sets of cogs mesh, and then you put a pen or pencil in one of the small holes of the wheel and trace out pattern as the wheel moves around and turns inside the circle. Must admit it is hard not to slip so lots of practice is definitely necessary! |  |
So here are some things for you to think about. It is
important to remember that it is the argument you use to justify
your decisions that is most important.
And a Wheel within a Wheel....
 |
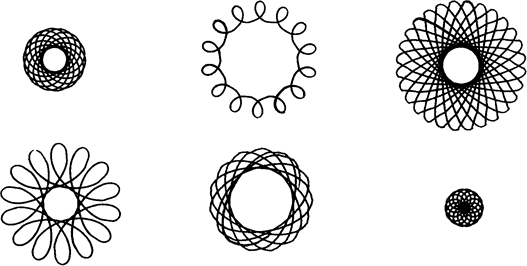
Below are pictures of six patterns I made with the toy. There are six patterns because I used all three wheels twice in circle A to produce them. One pattern was made with the pencil in the inner most hole of the spiral and one by placing the pencil in the outer-most hole. So two positions and three wheels makes six patterns. |
Can you work out which of the the three wheels with the pencil
in which position make each of the following patterns:
Never Ending or Beginning....
The following three patterns were made with each of the three
wheels. Can you work out which was made with the small, which with
the medium and which with the large wheel?
And here are a few more patterns to discuss. They are made
with any of the three wheels in one of the two circles with the
pencil in any one of the holes.
You may also like
Little Boxes
How many different cuboids can you make when you use four CDs or DVDs? How about using five, then six?