Skip over navigation
We're going to look at opening safes!
Many have dials on them, and you turn the dials - as you see in these two pictures - to open them.
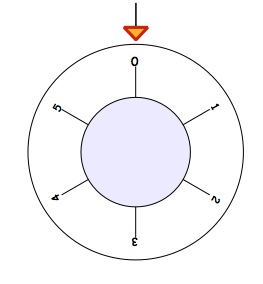
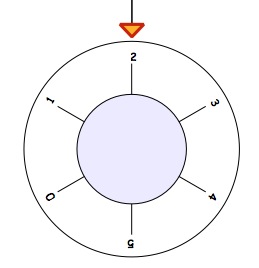
To open the safe, the dial has to have $2$ next to the arrow, like this;
The question for you is, how much turning of the dial did we have to do to get the $2$ at the top?
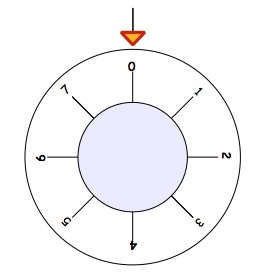
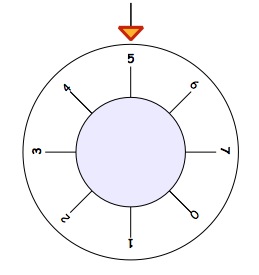
The next safe we get to has a different dial, it has the numbers $0 -7$.
How much turning to get the number $5$ at the top? [Shown in the second picture.]
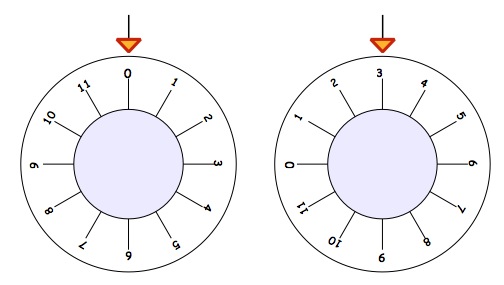
The number that you have to get at the top is often called the "combination" of the safe. These three different safes all start with $0$ [zero] at the top. You have to find the amount of turning to get to the combination, shown in each second picture:
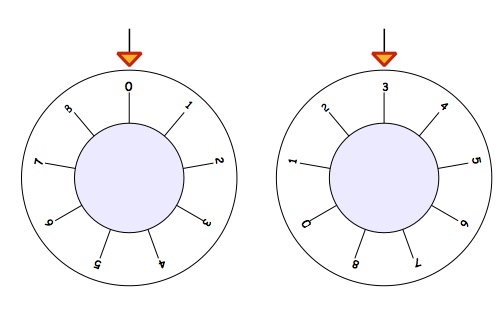
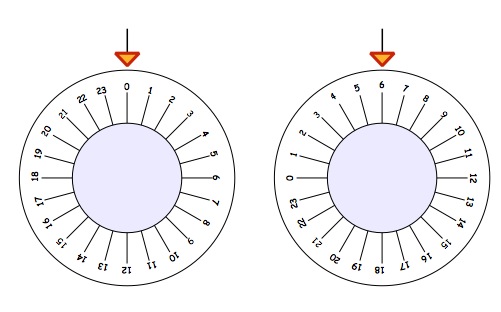
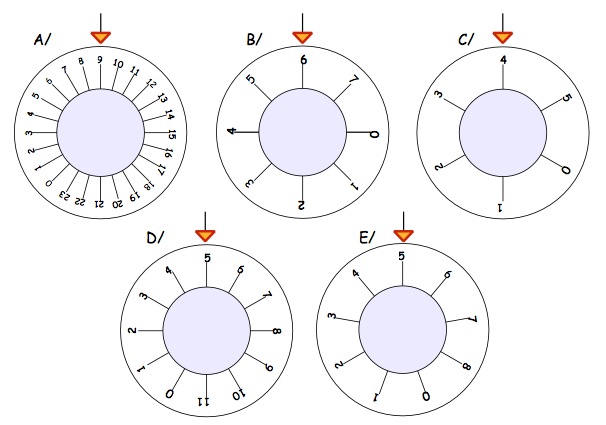
Now have a go at these different safes. Remember they would all start with $0$ [zero] at the top, so, how much turning to get the required combinations shown below?
How Safe Are You?
Age 7 to 11
Challenge Level 
How Safe Are You?
We're going to look at opening safes!
Many have dials on them, and you turn the dials - as you see in these two pictures - to open them.
So I'll show you a simple dial first with just the numbers $0 - 5$ on it.
To open the safe, the dial has to have $2$ next to the arrow, like this;
The question for you is, how much turning of the dial did we have to do to get the $2$ at the top?
The next safe we get to has a different dial, it has the numbers $0 -7$.
How much turning to get the number $5$ at the top? [Shown in the second picture.]
The number that you have to get at the top is often called the "combination" of the safe. These three different safes all start with $0$ [zero] at the top. You have to find the amount of turning to get to the combination, shown in each second picture:
Now have a go at these different safes. Remember they would all start with $0$ [zero] at the top, so, how much turning to get the required combinations shown below?
Why do this problem?
This activity is a rather different way of giving pupils some experience of turning and measuring angles in degrees. It may particularly appeal to those pupils who like visualising something real.
Possible approach
You might want to make a version of one of the dials out of two pieces of card, fixed in the middle with a paper fastener. In this way, you could ask the class to visualise the turning and offer their solutions with explanations, before checking their thoughts using the card model.
How this is approached and pupils' thoughts will vary a lot according to their age and experience. It might be alright for the youngest learners to give an answer that is an anticlockwise direction but they perceive it as clockwise, just because it's the numbers that are rotating. For older pupils it would be a good discussion point for them to consider in which direction the turning occurs.
Are their answers for anticlockwise or clockwise turning?
You could print out this sheet of the dials for children to work on in pairs.
Key questions
Which way are you rotating/turning your hand?
Is it more than half a full turn each time? Can you be more exact?
How many degrees there are in a circle?
Possible extension
Pupils with some knowledge of the $360^\circ$ complete turn will probably be able to have a go at the later questions. More advanced pupils would be able to create their own problems for other pupils to answer. They might like to use this image as a printable dial for those harder questions they may want to set.
Possible support
A circular protractor would be useful for some pupils. Some preliminary discussion could be had about the turning involved in an analogue clock.You may also like
Clock Hands
This investigation explores using different shapes as the hands of the clock. What things occur as the the hands move.
Watch the Clock
During the third hour after midnight the hands on a clock point in the same direction (so one hand is over the top of the other). At what time, to the nearest second, does this happen?
Take the Right Angle
How many times in twelve hours do the hands of a clock form a right angle? Use the interactivity to check your answers.