Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Inside Triangles



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Inside Triangles
Here is a four by four dotty grid:

I have joined three dots on the grid to make a triangle which has one dot inside it:
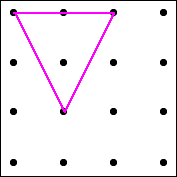
How many different triangles with one dot in the middle can you draw?
How do you know have found them all?
You may like to experiment with the pegboard interactivity below, or you could print off this page of dotty grids to work on.
Why do this problem?
This low threshold high ceiling activity is accessible to all pupils but has the scope to be extended in many directions. In order to make a start, children will need to be familiar with properties of triangles, but drawing triangles on the grid will help them to clarify for themselves what they understand by the term "triangle". In order to find all the possible triangles, pupils will need to work in a systematic way.
Possible approach
You may want to begin this task with the whole class and, this way, the notion of "different" will come up quite quickly. How is the group going to define "different"? This is a great discussion point and one where there isn't a right or a wrong answer. You could decide to count triangles which could be picked up and placed exactly on top of another triangle as the same. Or, you could decide that they are different if they are in a different orientation on the grid. The former suggestion makes a more manageable number to count!
Key questions
Tell me about the way you're working.
How will you remember which triangles you've found?
How do you know that your triangles are all different from each other?
How do you know that you have found them all?
Possible support
Having a range of different equipment available for children to use to tackle this problem (e.g. pegboards, grids on paper, the interactivity) will help everyone get started.
If learners are finding it difficult to work systematically, you could offer them 6 Beads and Three Ball Line Up first, which might be a more familiar context.
Possible extension
In order to extend the problem, pupils could be asked to find triangles with three spots inside them or no spots inside... Differently sized grids could be drawn and compared. You could sort the triangles across differently sized grids, for example all right-angled triangles together, or all triangles which are the same shape but different sizes together.
Related Collections
You may also like
Let's Investigate Triangles
Vincent and Tara are making triangles with the class construction set. They have a pile of strips of different lengths. How many different triangles can they make?

