Skip over navigation
Well, we're going to look at visiting places.
Here's the road map:
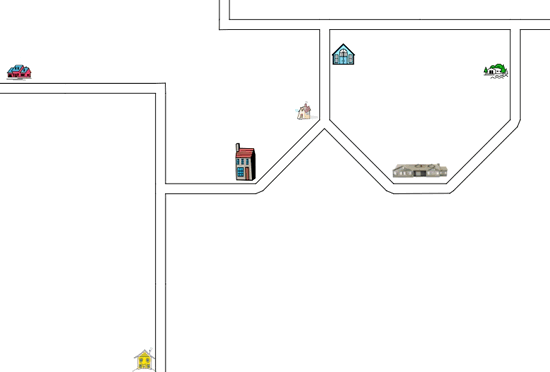
There are six places to visit:
1. Relations who live in the tall house;
2. Friends who live in the house with trees;
3. The wide school building;
4. The blue church;
5. The health centre with blue roof and pink walls;
6. The little pink shop which is leaning over.
You live in the yellow house at the bottom of the map.
Starting at your house, try to describe the journey to each of the six places.
You'll need to describe the bends in the road [how much they turn] and which way to turn at junctions.
Having done that what about trying this next one too:
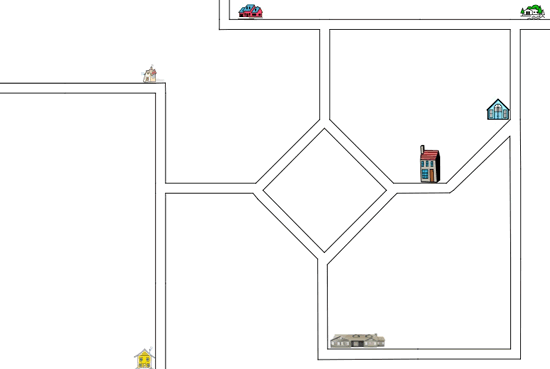
We have the same places to visit, but they are in different places now.
Six Places to Visit
Age 7 to 11
Challenge Level 
Six Places to Visit
Well, we're going to look at visiting places.
Here's the road map:
There are six places to visit:
1. Relations who live in the tall house;
2. Friends who live in the house with trees;
3. The wide school building;
4. The blue church;
5. The health centre with blue roof and pink walls;
6. The little pink shop which is leaning over.
You live in the yellow house at the bottom of the map.
Starting at your house, try to describe the journey to each of the six places.
You'll need to describe the bends in the road [how much they turn] and which way to turn at junctions.
Having done that what about trying this next one too:
We have the same places to visit, but they are in different places now.
Why do this problem?
This activity is a good one to try once children have some experience of turning and the measurement of the angles in degrees. It can also be an opener for looking at the angle turned rather than what might be called the internal angle.
Possible approach
This kind of activity can be best introduced by a pupil walking a path that requires some turning at junctions. You could set up a 'course' in the school hall or outside which involves going round obstacles, for example. You could then challenge pupils to imagine a bird's-eye view of the situation and sketch it. Then, a route could be drawn on the sketch and instructions given by one child
to direct another child along the route. This could be an opportunity for the class to develop the necessary language so that the instructions are accurate.
When working on the problem, it might be useful for children to have a copy of this sheet of the maps. The angles used are all multiples of $45^\circ$ so there will be no need for children to have protractors, rather they should be able to justify the amount
of turn for example by referring to fractions, or multiples, of a right angle.
Key questions
How much of a turn is there at this junction or bend in the road?
How are you finding the angles each time?
Possible extension
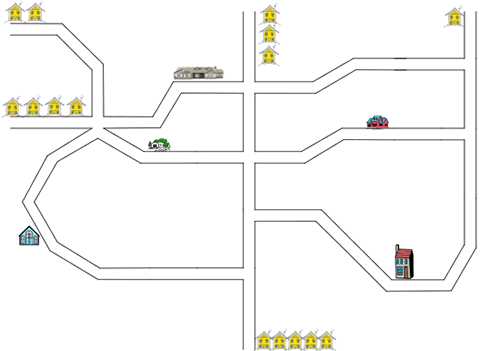
Older or more experienced pupils could try this third map with different places (where there are $1, 2, 3, 4$ or $5$ yellow houses) to start:
Here is a sheet to print which contains this map.
Childrencould find different lengths of routes to each of the five places to visit as well.
Possible support
Some of the play-mats that have road systems on them would be useful. A programable robot can be a useful aid as well.
You may also like
Clock Hands
This investigation explores using different shapes as the hands of the clock. What things occur as the the hands move.
Watch the Clock
During the third hour after midnight the hands on a clock point in the same direction (so one hand is over the top of the other). At what time, to the nearest second, does this happen?
Take the Right Angle
How many times in twelve hours do the hands of a clock form a right angle? Use the interactivity to check your answers.