Turning
Turning
Well, let's have a look at doing some simple turning.
To have a go at this task, you'll first need to make this 'interactivity' out of two differently-coloured discs of thick paper or card. Cut a slit into each from the edge to the centre in a straight line. Overlap the two slots and turn them to link the two discs together:
This YouTube Video shows how to make a similar thing with paper plates.
Can you turn your discs to show what:
a) a book being opened looks like from above?
b) turning a volume knob on your music player looks like?
c) a bicycle wheel looks like when going along?
d) a door would look like from above as it's being opened?
e) what a hamster wheel looks like when the hamster's running inside it?
Describe and then show some other things that you do or have seen, that turn in this way.
You can also have challenges that are just to do with the picture you see, for example, can you make the turning shape appear on the other side?
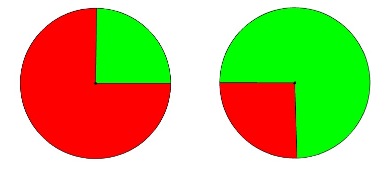
Can you make the red part twice the size of the green?
Why do this problem?
Possible approach
Show the class a ready-made 'interactivity' by manipulating it as they watch, talking through what you are doing. Depending on the class' age and experience, help them make the tool themselves, or give out some you have already made.
Children could then work in pairs, either at a computer, or with the card version. Encourage them to talk to each other as they try out their ideas.
Key questions
Tell me about what you are imagining.
How could we "check" what you have done?
Possible extension
Children could demonstrate a turn and challenge other children to select what it represents from, for example, a list of three scenarios.
Possible support
Some children will need to 'copy' the turning action of an item with their tool before they are confident at visualising.
You may also like
Biscuit Decorations
Andrew decorated 20 biscuits to take to a party. He lined them up and put icing on every second biscuit and different decorations on other biscuits. How many biscuits weren't decorated?