Twinkle Twinkle
This is a game for two players.
You need a one star game board and a set of four counters each.
To win, a player must place three of his/her own counters in a straight line.
To begin, each player takes turns to place one counter on an empty black spot.
Then, if no-one has yet made a line of three, play continues by taking turns to pick one counter and move it to an empty black spot.
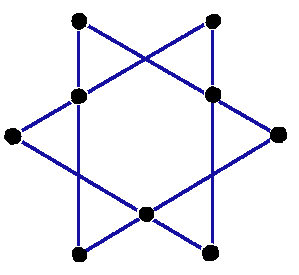
What moves will increase your chance of winning?
Does it matter who goes first?
Is it possible to play an 'endless' game?
Printable NRICH Roadshow resource.
You may also like
Traffic Lights
The game uses a 3x3 square board. 2 players take turns to play, either placing a red on an empty square, or changing a red to orange, or orange to green. The player who forms 3 of 1 colour in a line wins.
Yih or Luk Tsut K'i or Three Men's Morris
Some puzzles requiring no knowledge of knot theory, just a careful inspection of the patterns. A glimpse of the classification of knots and a little about prime knots, crossing numbers and knot arithmetic.