Blockupied
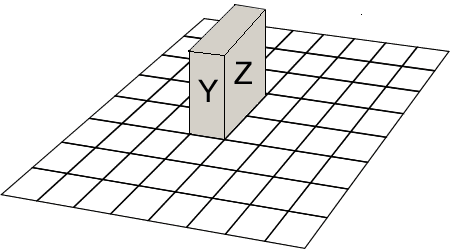
A $1\times2\times3$ block is placed on an $8\times8$ board, as shown with the $1\times2$ face $X$ at the bottom.
It is rolled over an edge, without slipping, onto a $1\times3$ face $Y$, then onto the $2\times3$ face $Z$, then onto $X$, $Y$, $Z$ again in that order.
How many different squares on the board has the block occupied altogether, including the starting and ending positions?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Tea Cups
Place the 16 different combinations of cup/saucer in this 4 by 4 arrangement so that no row or column contains more than one cup or saucer of the same colour.
Counting on Letters
The letters of the word ABACUS have been arranged in the shape of a triangle. How many different ways can you find to read the word ABACUS from this triangular pattern?