Hamiltonian Cube

Visiting all the vertices

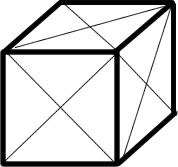
The figure shows a cube with sides of length $1$, on which all twelve face diagonals have been drawn - creating a network with $14$ vertices (the original eight corners, plus the six face centres) and $36$ edges (the original $12$ edges of the cube plus four extra edges on each face). What is the length of the shortest path along the edges of the network which passes through all $14$ vertices?

If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.