Semicircle in a Semicircle
Let T be the centre of the semicircle with diameter QR and let OT produced meet the circumference of the larger semicircle at U .
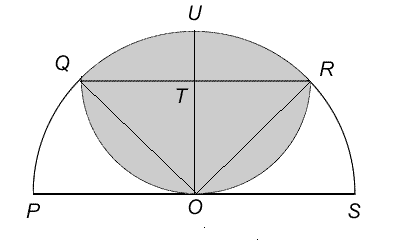
By symmetry, we note that OT is perpendicular to QR . As TR = TO = TQ (radii of the same semicircle), triangles ORT and OQT are both isosceles, right-angled triangles. So QOR is a right angle.
By Pythagoras' Theorem: QR ² = OQ ² + OR ² = 2 ² + 2 ² = 8. So $QR = \sqrt8$ = $2\sqrt2$ and the radius of semicircle QOR is $\sqrt2$.
You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Polycircles
Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?
Circumspection
M is any point on the line AB. Squares of side length AM and MB are constructed and their circumcircles intersect at P (and M). Prove that the lines AD and BE produced pass through P.