Shaping the Universe I - Planet Earth

For thousands of years mankind has been trying to work out the shape and structure of the universe we live in. Is the earth flat or round? Do the planets orbit around the Earth or the Sun? What shape are their orbits? Where are the stars in relation to the planets? Mathematics has always been crucial for this endeavour. It's all very well looking up at the stars, but you need mathematical theories and systems to make sense of it all. Much of the history of astronomy concerns the use of the most basic shapes - circles, spheres etc - and yet people have disagreed enormously because of our inability actually to see what shape things are. This is the first in a series of articles exploring how astronomers over the ages have tried to visualise the cosmos around us.

Pythagoras, like many Ancient Greeks, believed that circles and spheres were the most perfect shapes and therefore that the earth and all the heavenly objects must be spherical. So his model was based on aesthetic reasoning - he believed that the most beautiful and 'harmonious' shape must be the true shape of the earth. He did not attempt to prove it, because it just seemed natural that the world should be geometrically perfect. If you could imagine the world being any other shape that you think is beautiful, what would it be? How could you test whether or not it was the right shape without travelling all the way around the world or looking at it from space? Have a look at some different earth shapes here . To find out more about Pythagoras see our previous articles here and here .

Aristotle also believed that the world was spherical, but he used observations to prove that it was true. He pointed out that when the earth casts a shadow on the moon during a lunar eclipse, the shadow is always circular. Can you think why this proved that the earth was a sphere? Try visualising what the shadow would look like if the earth was a flat disc. What would happen to the shadow if you tilted or rotated the disc in different directions? You could even try this with a lamp in a darkened room and some different shapes to represent the earth.



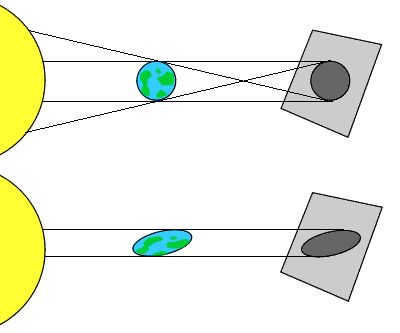
As you can see then, the only shape that would always cast a circular shadow is a sphere. Aristotle also noticed that people could see different stars and constellations depending on how far north or south they were, so that also suggested that the earth was spherical.

If you have seen the film Pirates of the Caribbean: at world's end , where the ship falls off the edge of the world over a giant waterfall, then you will know that a lot of people used to think the earth was flat. Even though astronomers knew that it was round, it didn't convince a lot of ordinary folk who were frightened of sailing too far and falling into oblivion. Can you think of some reasons why the idea of a flat earth seemed so plausible to so many people?

Today we know that the earth is spherical because we have been able to measure its curvature very accurately and even see it from space. However we also know that it isn't a perfect sphere, and this was predicted by Isaac Newton as a consequence of his theory of gravitation. In fact the earth bulges out slightly around the middle, and is slightly flatter at the north and south poles.
 

The next instalment in this series of articles is Shaping the Universe II - The Solar System , where we shall be looking at how astronomers over the ages visualised and modelled the other planets and objects surrounding the Earth.