Skip over navigation
Answer: 36
1 by 1 squares:
Must contain an even number
Up to 25 there are 12 even numbers
2 by 2 squares:
examples: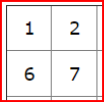
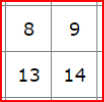
2 by 2 squares always contain 2 even and 2 odd numbers so all have an even total
2 by 2 squares can't have their first number in the last row or column, so there are 16 2 by 2 squares in the grid
3 by 3 squares:
They can have 4 odd numbers or 5 odd numbers
5 odd numbers means the sum is odd, 4 odd numbers means the sum is even
3 by 3 squares containing 4 odd numbers begin on even numbers
How many are there in the grid? The square starting at 6 is good but the one starting at 14 is not
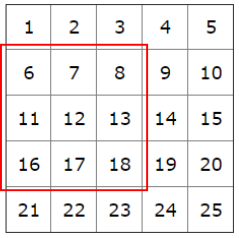
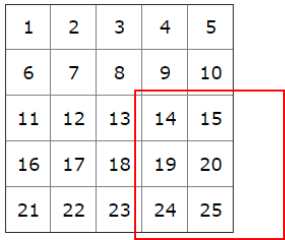
The 3 by 3 square can start at 2, 6, 8 or 12 (4 possible)
4 by 4 squares:
These contain 8 even numbers and 8 odd numbers (they are 4 2 by 2 squares stuck together)
There is one in each corner of the whole square (4 possible)
5 by 5 squares:
Not allowed - the grid contains 12 even and 13 odd numbers
Total: 12 + 16 + 4 + 4 = 36
Even Squares
Age 11 to 14
ShortChallenge Level 
Answer: 36
1 by 1 squares:
Must contain an even number
Up to 25 there are 12 even numbers
2 by 2 squares:
examples:
2 by 2 squares always contain 2 even and 2 odd numbers so all have an even total
2 by 2 squares can't have their first number in the last row or column, so there are 16 2 by 2 squares in the grid
3 by 3 squares:
They can have 4 odd numbers or 5 odd numbers
5 odd numbers means the sum is odd, 4 odd numbers means the sum is even
3 by 3 squares containing 4 odd numbers begin on even numbers
How many are there in the grid? The square starting at 6 is good but the one starting at 14 is not
The 3 by 3 square can start at 2, 6, 8 or 12 (4 possible)
4 by 4 squares:
These contain 8 even numbers and 8 odd numbers (they are 4 2 by 2 squares stuck together)
There is one in each corner of the whole square (4 possible)
5 by 5 squares:
Not allowed - the grid contains 12 even and 13 odd numbers
Total: 12 + 16 + 4 + 4 = 36
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Painting Cubes
Imagine you have six different colours of paint. You paint a cube using a different colour for each of the six faces. How many different cubes can be painted using the same set of six colours?
Tri-colour
Six points are arranged in space so that no three are collinear. How many line segments can be formed by joining the points in pairs?
Cube Paths
Given a 2 by 2 by 2 skeletal cube with one route `down' the cube. How many routes are there from A to B?