Skip over navigation
Ever been to a Hotel only to find that it is full? The problem is that it has only got a finite number of rooms, and so they can quickly get full. However, Hilbert managed to build a hotel with an infinite number of rooms. Below is the story of his hotel.
When the Hotel first opened, everything went fine. He had lots of visitors. He gave the first person room 1, the second person room 2, and so on. This worked well until he found that one day after a very busy week the Hotel was full (so there were now an infinite number of people staying in the hotel).
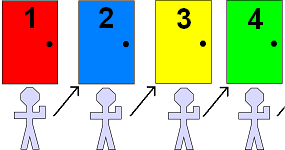However, he had a solution. He went on the loud speaker, and asked
everyone in the hotel if they could move to the next room number
after theirs. So the person in room 1 moved into room 2, the person
in room 100 moved into room 101, and so on. The new guests were
then given room 1.
Things were going well, until one day a tour company had an idea - and started sending buses which contained an infinite number of people. In fact, they sent an infinite number of buses (numbered 1, 2, 3 etc.) Struggling to work out what to do, he asked his friend Cantor for some help:
The plan worked perfectly, soon everyone had got off the bus and had a room in the hotel.
Hilbert was very pleased because he thought that he would be able to use Cantor's method to allocate rooms to any number of visitors. However, Cantor warned him that there might be situations when it would be impossible to find a way of allocating rooms.
Hilbert found that difficult to believe. If you would like to read more about Cantor's arguments, you might like to read the article Infinity Is Not a Number - It's a Free Man .
Hilbert's Hotel
Ever been to a Hotel only to find that it is full? The problem is that it has only got a finite number of rooms, and so they can quickly get full. However, Hilbert managed to build a hotel with an infinite number of rooms. Below is the story of his hotel.
When the Hotel first opened, everything went fine. He had lots of visitors. He gave the first person room 1, the second person room 2, and so on. This worked well until he found that one day after a very busy week the Hotel was full (so there were now an infinite number of people staying in the hotel).
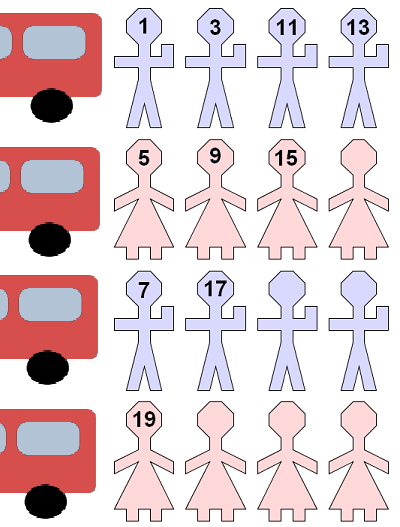
Things were going well, until one day a tour company had an idea - and started sending buses which contained an infinite number of people. In fact, they sent an infinite number of buses (numbered 1, 2, 3 etc.) Struggling to work out what to do, he asked his friend Cantor for some help:
"Simply ask everyone to move into
the room whose number is twice the number of that they are
currently in. Now all the odd numbered rooms are empty. Now assign
the first person in the first bus room 1, the second person in the
first bus room 3, then the first person in the second bus room 5,
and carry on in the same manner picking one person from each bus as
you walk up and down pass the row of buses, picking people from one
more bus each time."
The plan worked perfectly, soon everyone had got off the bus and had a room in the hotel.
Hilbert was very pleased because he thought that he would be able to use Cantor's method to allocate rooms to any number of visitors. However, Cantor warned him that there might be situations when it would be impossible to find a way of allocating rooms.
Hilbert found that difficult to believe. If you would like to read more about Cantor's arguments, you might like to read the article Infinity Is Not a Number - It's a Free Man .
Related Collections
You may also like
How Many Elements Are There in the Cantor Set?
This article gives a proof of the uncountability of the Cantor set.