IFFY Triangles

Nayanika from The Tiffin Girls' School and Ben from Thomas Hardye, both in the UK, both proved the first pair of statements, and an anonymous solution combined the two statements into a single 'if and only if' statement.

This is Nayanika's proof for statement 1a (if $A,B$ and $C$ are in an arithmetic progression, then $B=60^\circ$):

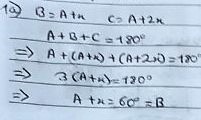
This is Ben's proof for statement 1b (if $Y=60^\circ,$ then $X, Y$ and $Z$ are in an arithmetic progression):

Ben's proof is good, but the final statement is actually the wrong way around. Ben started by assuming that $Y=60,$ and showed that whenever $Y=60,$ $X,Y$ and $Z$ form an arithmetic progression. This is written as $$Y=60\Rightarrow X,Y,Z\text{ form an arithmetic progression}$$

An anonymous solution combined this pair of statements into a single 'if and only if' statement:

Therefore, $ABC$ is a triangle with angles $A,B$ and $C$ where $A\lt B\lt C$ $$A,B,C \text{ form an arithmetic progression}\iff B=60$$

Ben and Nayanika both sent in proofs for the second pair of statements, and the anonymous solution combined them into a single 'if and only if' statement.

Ben proved statement 2a (that in a triangle $PQR,$ if the lengths $PQ$ and $QR$ are equal, then angles $P$ and $R$ are equal):

To confirm that the perpendicular bisector to side $PR$ really does pass through $Q$ and $S,$ note that $Q$ and $S$ are both equidistant from $P$ and $R.$

Nayanika proved statement 2b (that in a triangle $KLM,$ if angles $K$ and $M$ are equal, then lengths $KL$ and $LM$ are equal) using congruence:

Ben proved statement 2b using trigonometry:

Once again, the anonymous solution combined the two statements into one single 'if and only if' statement:

Therefore, PQR is a triangle $$PQ = QR \iff \hat{P} = \hat{Q}$$