Skip over navigation
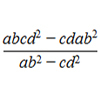
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Expenses
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This problem has two steps. Students may be familiar with factorisation methods for finding divisors but in this situation the numbers do not divide exactly but instead have a common remainder - providing an opportunity for students to look for a step which will allow them to apply something familiar in a new and extending case.
You may also like
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.

