Skip over navigation
You may want to look at Overlaps before you try this problem.
Here are some pairs of shapes:
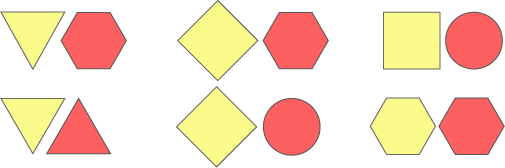
What overlap shape would you get if you overlapped them halfway across each other?
Here are some more pairs of shapes. What overlap shapes would you get this time?
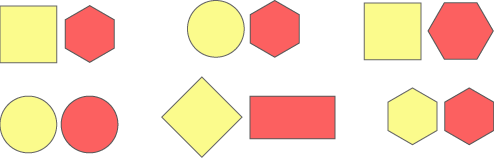
Which of these overlap shapes did you find?
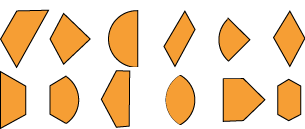


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Overlapping Again
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Overlapping Again
You may want to look at Overlaps before you try this problem.
Here are some pairs of shapes:

What overlap shape would you get if you overlapped them halfway across each other?
Here are some more pairs of shapes. What overlap shapes would you get this time?

Which of these overlap shapes did you find?
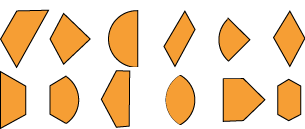
Why do this problem?
This problem, as Overlaps, focuses on encouraging children to visualise - in this case to picture an image in their head. There are also valuable opportunities for them to apply their knowledge of properties of shape, and to use appropriate vocabulary.
Visualising can be a very useful way of getting into a problem, but it can also help at other stages of the problem-solving process. Providing opportunities like this for your class to practise visualising will help them to become familiar with its uses and to regard it as a legitimate skill to draw upon.
Key questions
What are the two shapes you are thinking about?
Looking at the overlaps where the sides are diagonal, which shapes could they have come from?
Can you imagine gradually moving one shape across the other one?
Possible extension
Learners who need more of a challenge could try Quadrilaterals.
Possible support
Suggest trying this simpler version of the problem.
You may also like
Four Triangles Puzzle
Cut four triangles from a square as shown in the picture. How many different shapes can you make by fitting the four triangles back together?
Playground Snapshot
The image in this problem is part of a piece of equipment found in the playground of a school. How would you describe it to someone over the phone?

